以前、
背理法
で大体解けるんじゃないかという仮説を立ててみて、その際に、
「できるだけ別の候補の数を減らしてからのほうが望ましい」
と書いたのだが、しかし現実はそうもいかない。
候補の数が3つも4つもあるのに、何一つ決まらない、ということが頻繁に起きてくる。
そこで、そのような状態で背理法を使うには? ということを模索していて、ある程度カンがつかめてきたので、ここで紹介する。
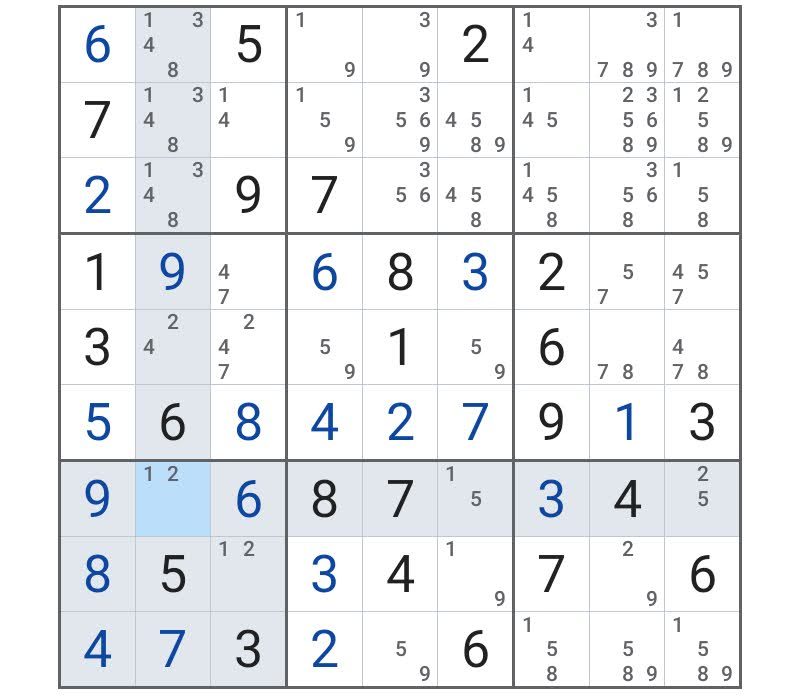
まず冒頭の画面の再掲。

なんと、すごいところは、「候補の数」が6つもある!
しかしながら、この状態で何も決まらない、という困った状況である。
もちろん「2マスの専有の数」および「3マスの専有の数」は減らしておいたのに、この有り様である。
(注:2つのマスに「a、b」の候補があったら、その2マスで「a、b」は専有できるので、他のマスから「a、b」を削除できる。
これを拡張させて、3つのマスに「a、b、c」の数が2つ以上あったら、その3マスで「a、b、c」は専有できる。
(例:「1、3」「1、5」「1、3、5」のマスがあったとしたら、その3マスで「1、3、5」は埋まり、他のマスに「1、3、5」が入ることはない)
詳しくは「ナンプレ(ライブ)1」を参照されたい。
さらに、あまり使う機会はないが、4つのマスに「a、b、c、d」の数字が2つ以上あるとその4マスを専有できる。
(例:「1、2」「1、3、4」「2、3」「1、2、3、4」というマスがあったとしたら、この4マスで「1、2、3、4」を専有でき、他のマスから削除できる。
理由:細かい場合分けはしないが、「3マス専有」のケースに還元できるから。
上記の例でいえば、
- 最初のマスを「1」とすると、「1」「3、4」「2、3」「2、3、4」となって、後半3つが「3マス専有」のケースになる。
- 最初のマスを「2」とすると、「2」「1、3、4」「3」「1、3、4」→「2」「1、4」「3」「1、4」となって、やはり後半3つが「3マス専有(2マス専有)のケースに還元できる。
となる。
そして、「4マス専有」を使う機会があまりない、というのは、「4マスが埋まったら残りは5マスなので、大体すでに埋まっているから」である。
というわけで、
「専有が確定していない段階で背理法はどの程度有効か」
ということを書いてみたい。
もちろん、「背理法」を使うには、数の候補が少ないほうがいいのだが、これまでやってきたケースでは「数字3つ」というものもあったが解けた。今回は「数字2つのケース」で書いてみる。
ということで、赤で囲ったところに注目する。
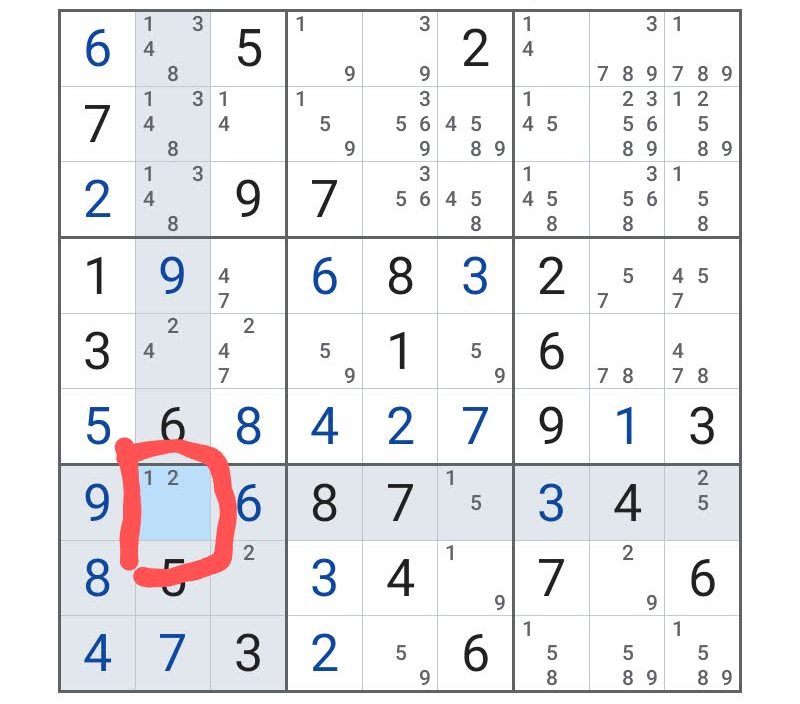
この部分を、仮に「1」と仮定してみる。
すると、こうなる。
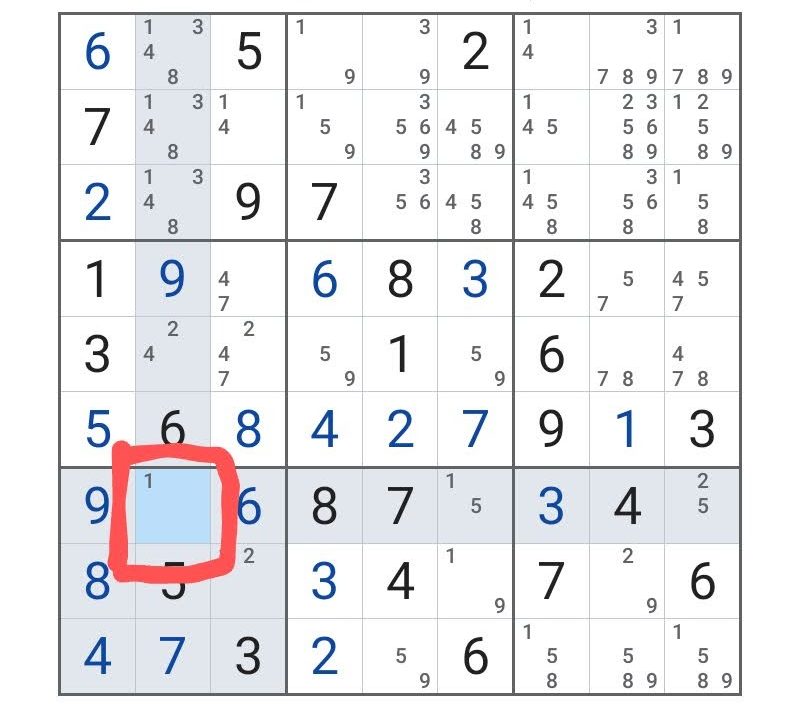
で、ここを「1」だとした場合に確定するものをとにかく確定していく。いかに「ここは関係なさそう?」と思っても、ひたすら確定できるところは確定し、定まらないものは放っておく。
するとこうなった。
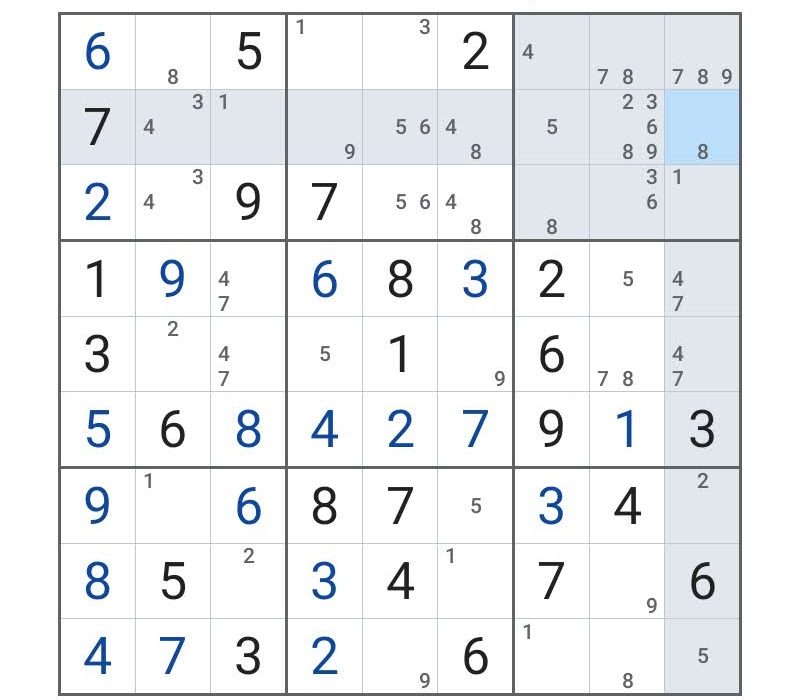
いろいろ定まらないところは多いものの、ここで決定的な事が起きている。
赤で囲ったところを見てみよう。
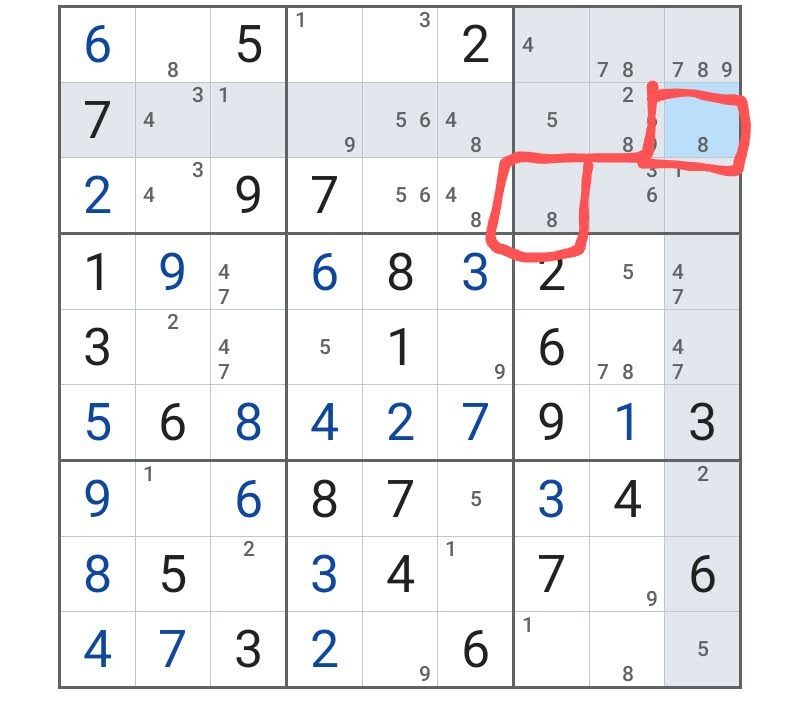
同じ正方形の中に、「8」が2つある
のだ。
これは明らかに矛盾なので、「元に戻す(Undo)」機能を使い、最初のマスが「1、2」の2つの候補になるまで戻り、ここを「2」とする。
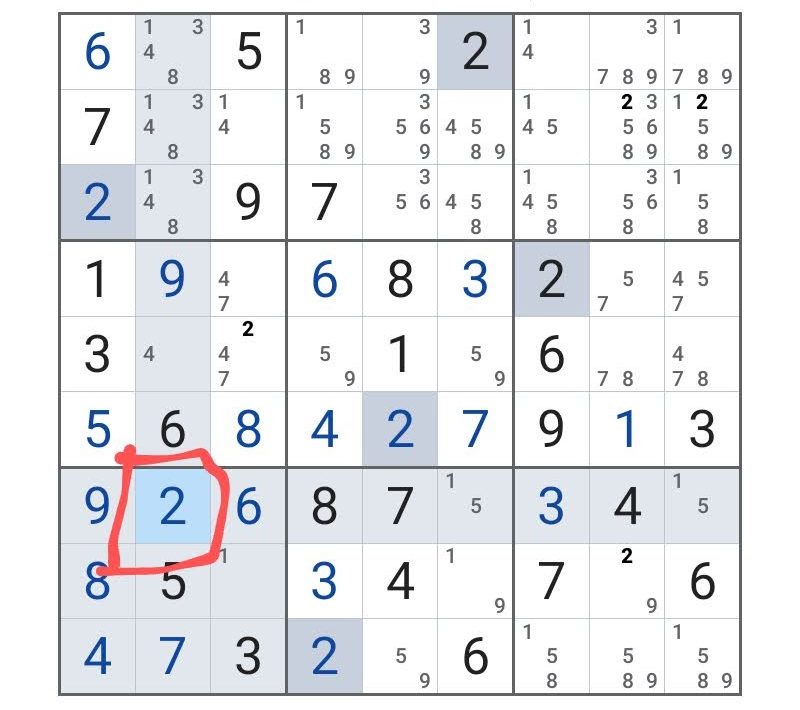
やはり「2」で合っていたわけだ。
ここを「2」とした状態で、残りのマスを埋められるだけ埋めていき、再び行き詰まったらまた背理法を使うのだが、
今回はここだけが決まったら最後まで行った。
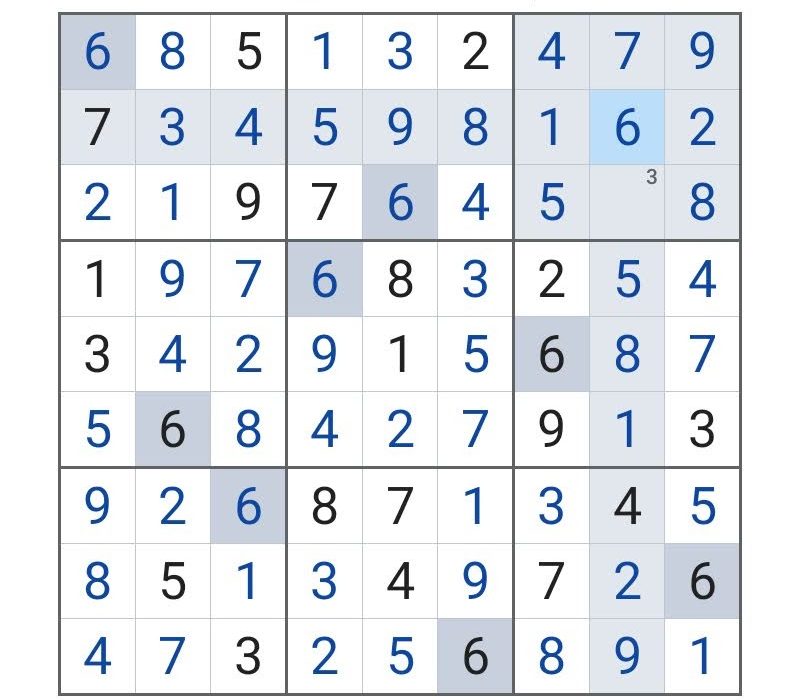
これで完成!
本来「メモ機能」はこう使うものではないのかもしれないのだが、法則性を自分で探していく作業というのは存外に楽しい。
また、「ナンプレは数学」と以前書いたが、よくよく考えてみたら計算をしないし、
「123456789」ではなく、
「abcdefghi」でもよいわけなので、「数学かな?」というところはあるが、考え方に数学を応用しているとは言えるかもしれない。
ジャンルとしてはやはり「パズル・ゲーム」という感じだろうか。
なお、「ナンプレは脳によいか?」といった記事を以前見つけたのだが、紆余曲折あって、
かつては脳トレ的なものは脳によいといわれてきたが2018年に「別によくはない」とされ、2019年に一転「やはり脳によい」ということになった
とのことである。
★うつの真実⑨→脳トレの代表格「ナンプレ」は「うつ病予防」に最適?→論理的思考力の向上
どうも、解けたときの爽快感が、何やら頭に快楽物質が流れてくる感じがして、これが(脳の)健康に一役買うのではないか、と個人的には思っている(学説的にはどうだかわからないが)。


コメント