しばらくナンプレをやるのをやめていた。
というのは、初級、中級、上級、エキスパートときて、毎日エキスパートをやっていたら、常勝無敗になったので興味をなくしてしまったのである。
ところがある日、「別のアプリだとどのような難易度だろうか」と思い、別のナンプレアプリを入れてみた。
このアプリには「エキスパート」より上の「エクストリーム」というクラスがあった。これは、難しかった。
久しぶりに「1問解くのに2時間かかる」という経験をした。
そして再び、毎日1~2問ずつ解く生活が始まった。そのうちに、「エキスパート」以下ではやらなくてもよかった新しい解法を編み出したので、それを紹介しようと思う。
(現在、「エクストリーム」クラスにおいて199勝中なので、間違ってはいないと思う)
これまでのエキスパート以下のクラスで通用したテクニックはもちろんそのまま使う。
- 2マス占有の法則
数字a、bが2マスにあれば、その2マスでそのabを占有できる。
例:「1、3」「1、3」というマスがあったとしたら、同じ列、同じ正方形から1と3は除外できる。 - 3マス占有の法則
2マスと同様に考えて、数字3つ(以下)が3マスにあった場合、その3マスで3つの数字を占有できる。
例:「1、2、3」「1、3」「2、3」というマスがあったら、その3マスで「1、2、3」を占有するため、同じ列、同じ正方形から「1、2、3」を除外できる。
2マスのときは証明もいらないが、こちらは必要。要するにどれか1つを確定すれば残り2マスも一意に決まるか、あるいは2マス占有のケースと同じになるためである。
気が付きにくいが、これも3マス占有の例:「1、2」「2、3」「1、3」。
最初のマスを「1」とすると次のマスが「2、3」、その次が「3」となるから、2番目が「2」と決まる。 - 同様に、4マス占有、5マス占有とあるが、4マスはエクストリームでは使うが、5マス占有はほぼ使わない。
- 9*9マスの普通のナンプレにおいては正方形が9つできるが、縦と横の列において一つの数字がどの正方形に属するか決まれば、他の正方形からは除外できる。
- 行き詰まったら、候補の数が2つのマスを基点として仮定法で「仮にここは~~である」と決めてある程度進み、矛盾が生じたら仮定をしたところまで戻り、もう一つの候補数に決める。
ここまでがこれまで使ってきたテクニック。そして今回紹介するのは、「どれほど候補の数が増えても使える」という方法である。
- 候補数が少ないマスに注目するのではなく、9つの正方形のうち、例えば「9」なら「9」のはまる候補が2つしかない正方形に着目し、どちらかを仮に「ここは9である」として仮定法を行う。
という方法である。
では順を追ってみてみよう。
まずは初期画面。

これが初期画面。そして、とりあえずはまる候補の数を全部埋めたものが次になる。
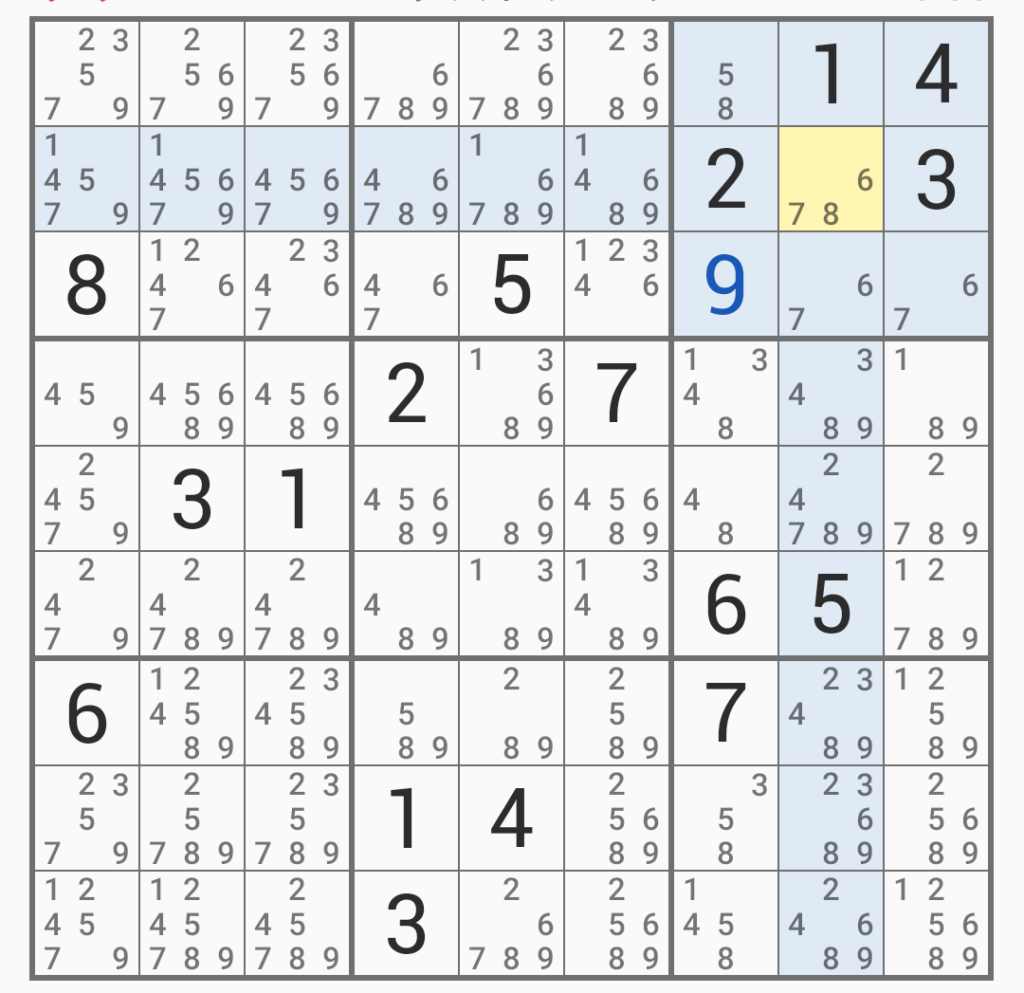
で、ここから将棋でいうところの「整地」をしていく(なお、私は将棋は全然ダメである)
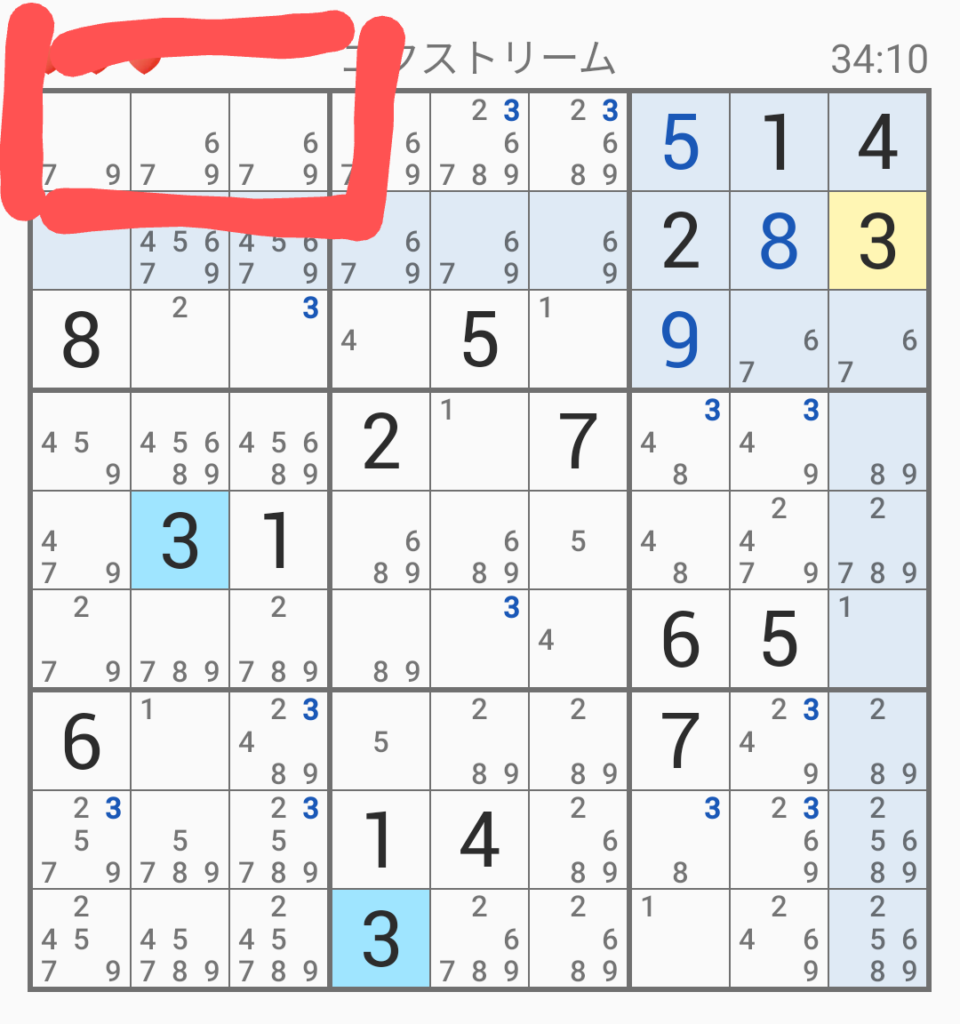
ここでは、赤で囲ったところを見てほしい。
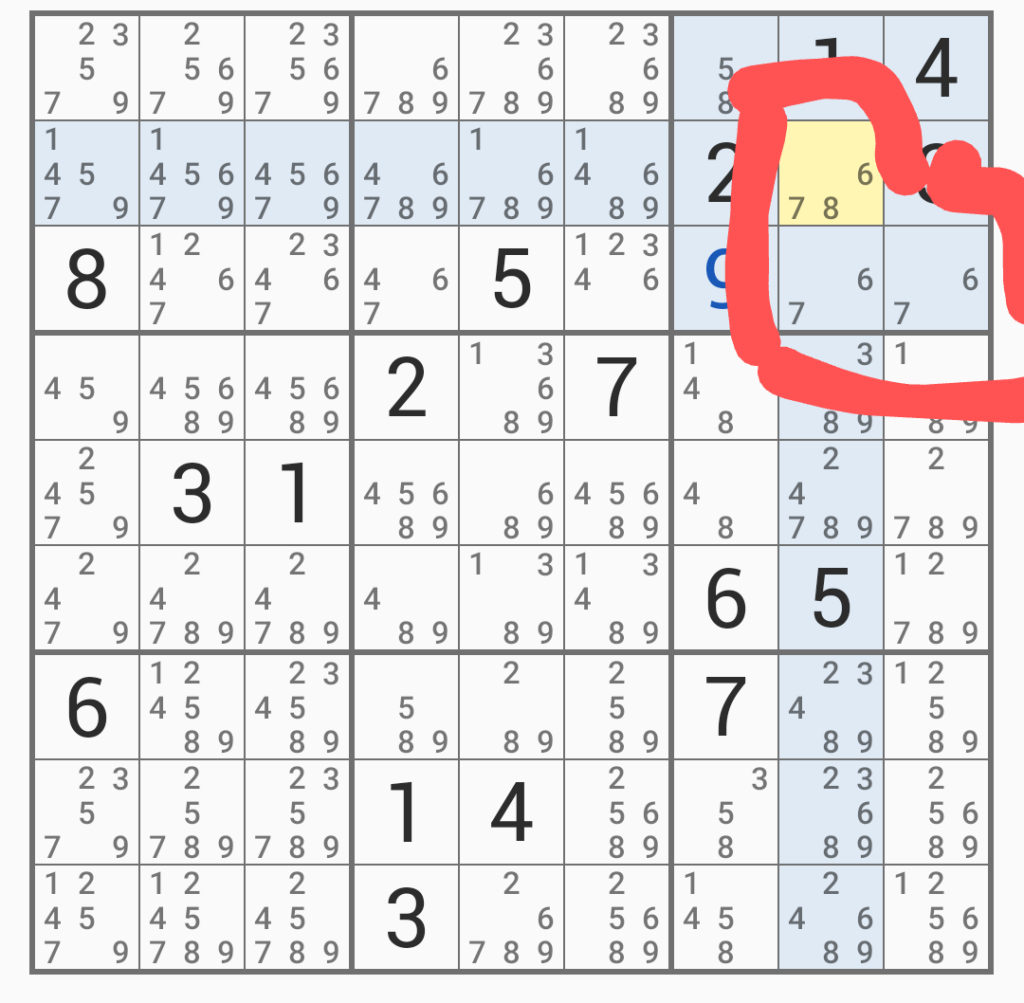
「6、7、8」「6、7」「6,7」なので、「6、7」のマスはこの2マスで決まるため、「6、7、8」のとところは「8」になる。
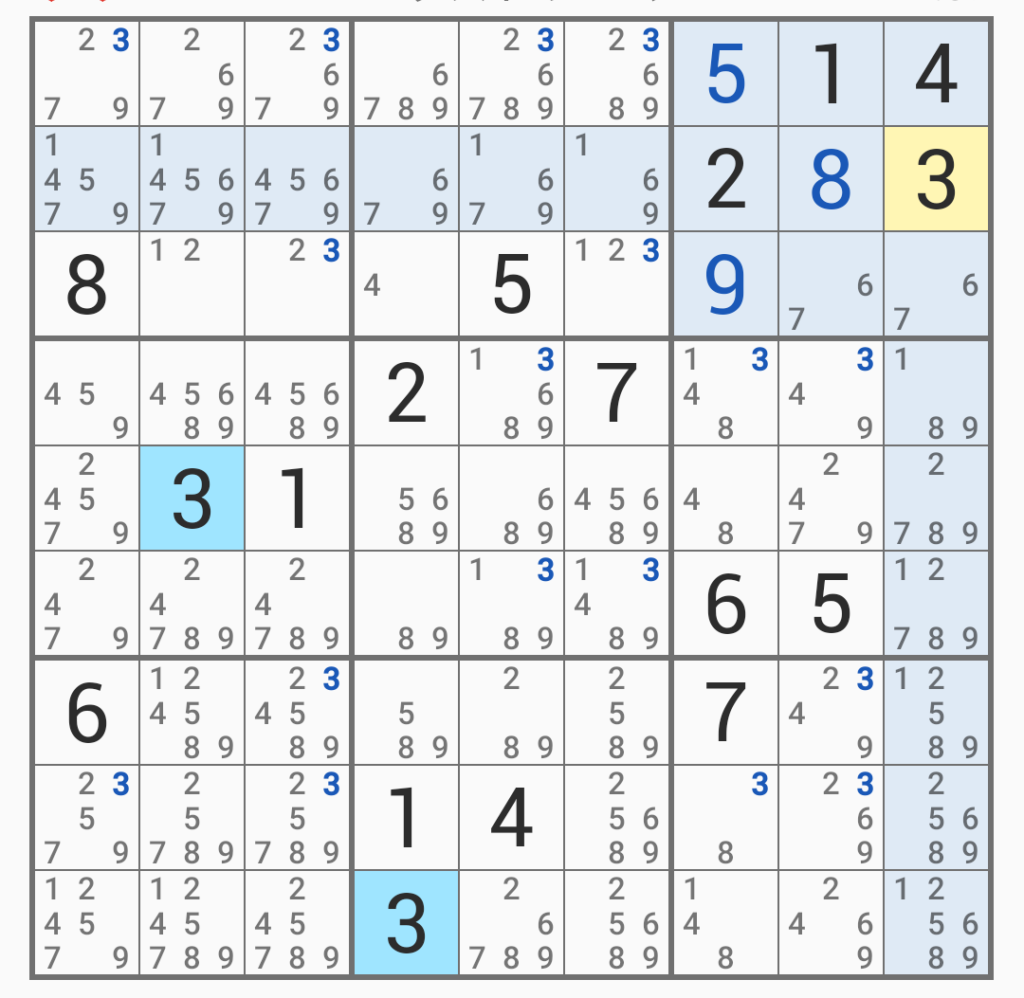
すると今度は「6、7」の列において「6、7」は除外できるため、それを消すと上記のようになる。
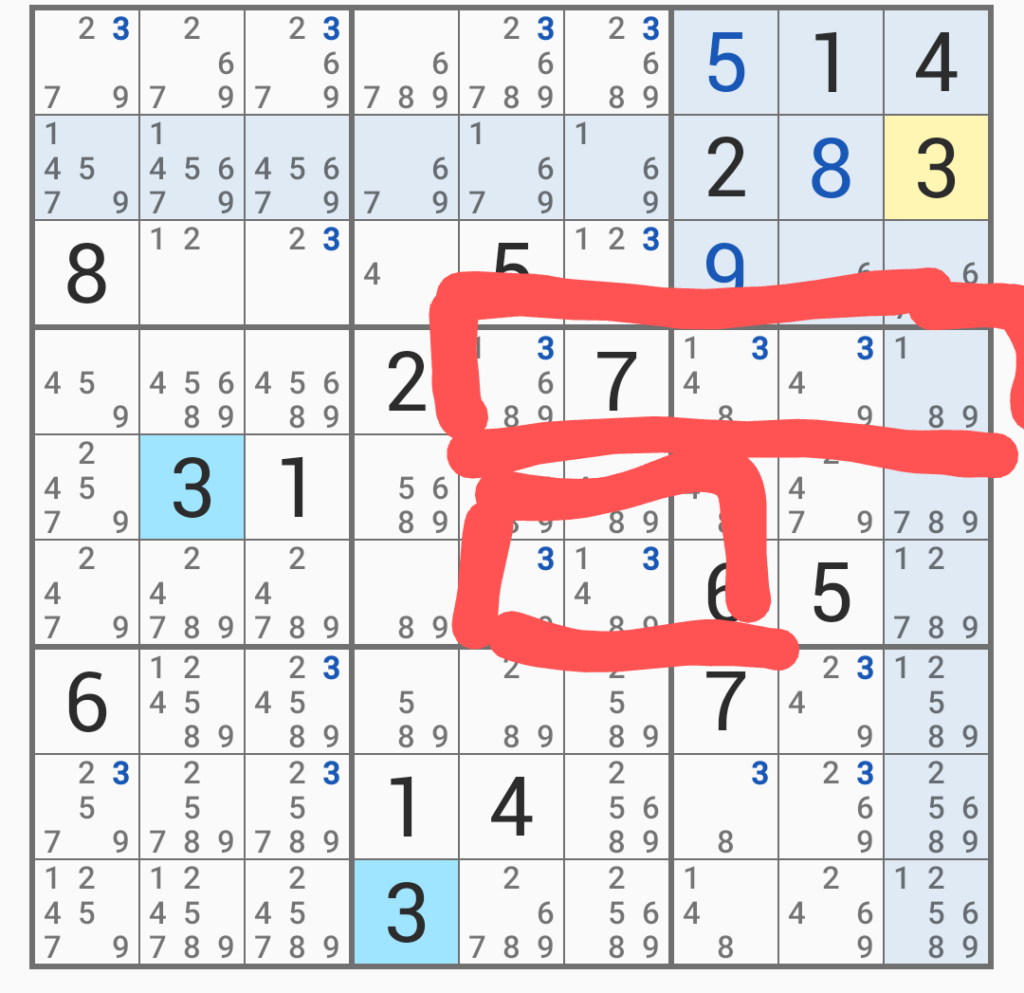
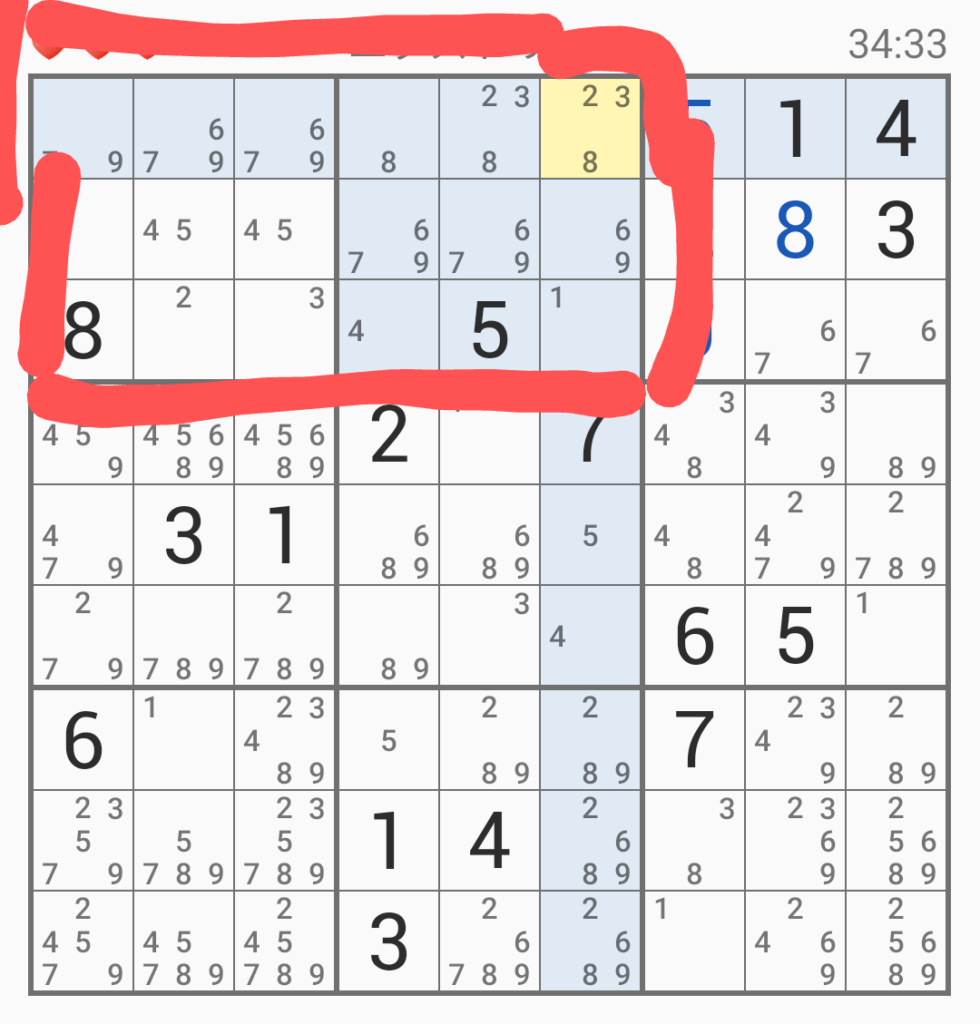
次に赤で囲ったところに注目すると、右端の正方形は一番上にしか「3」がないため、この列はここで決定となる。そのため、中央の正方形の上にある「3」は除外できる。
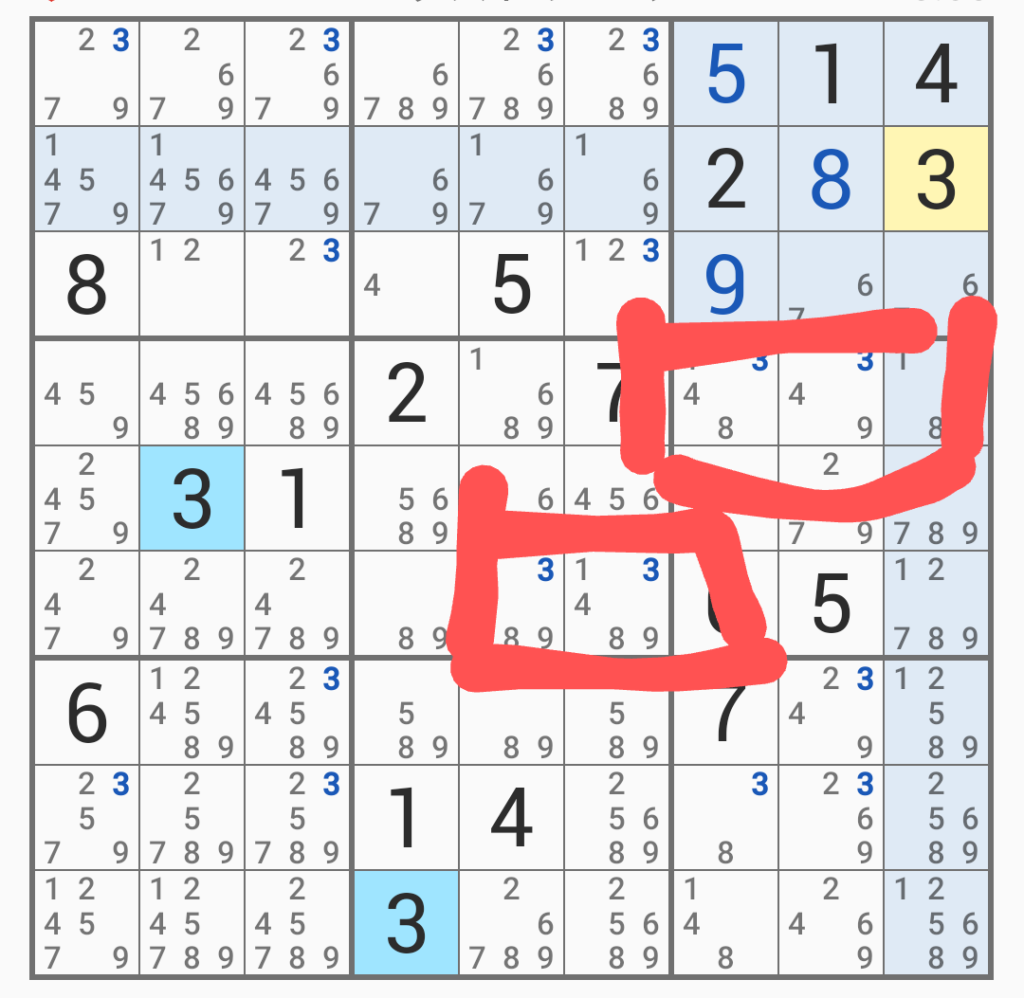
すると、こうなる。
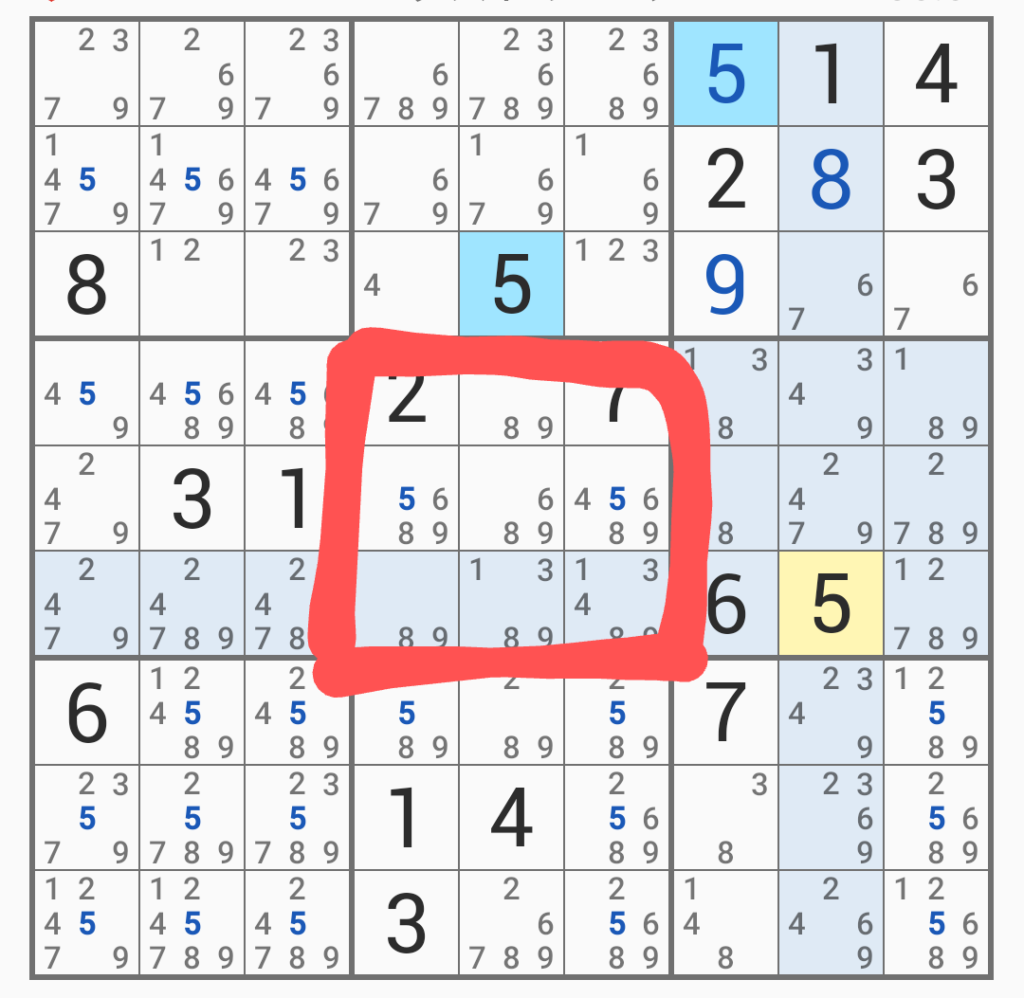
ここで少し行き詰まりを感じたので、例の「新しい方法」を使う。
これまで私が行ってきた方法では、
「1マスの数字の候補が2つのところ」を基点として仮定法を使っていたが、今回はそうではなく、
「ある数字に着目して、その数字が正方形内に2つあるところを探し、どちらかを基点とする」というやり方でいく。
赤で囲ったところで、特に「5」に注目すると、ここは「5」の候補が2つしかないので、ここではじめてみようと思う。
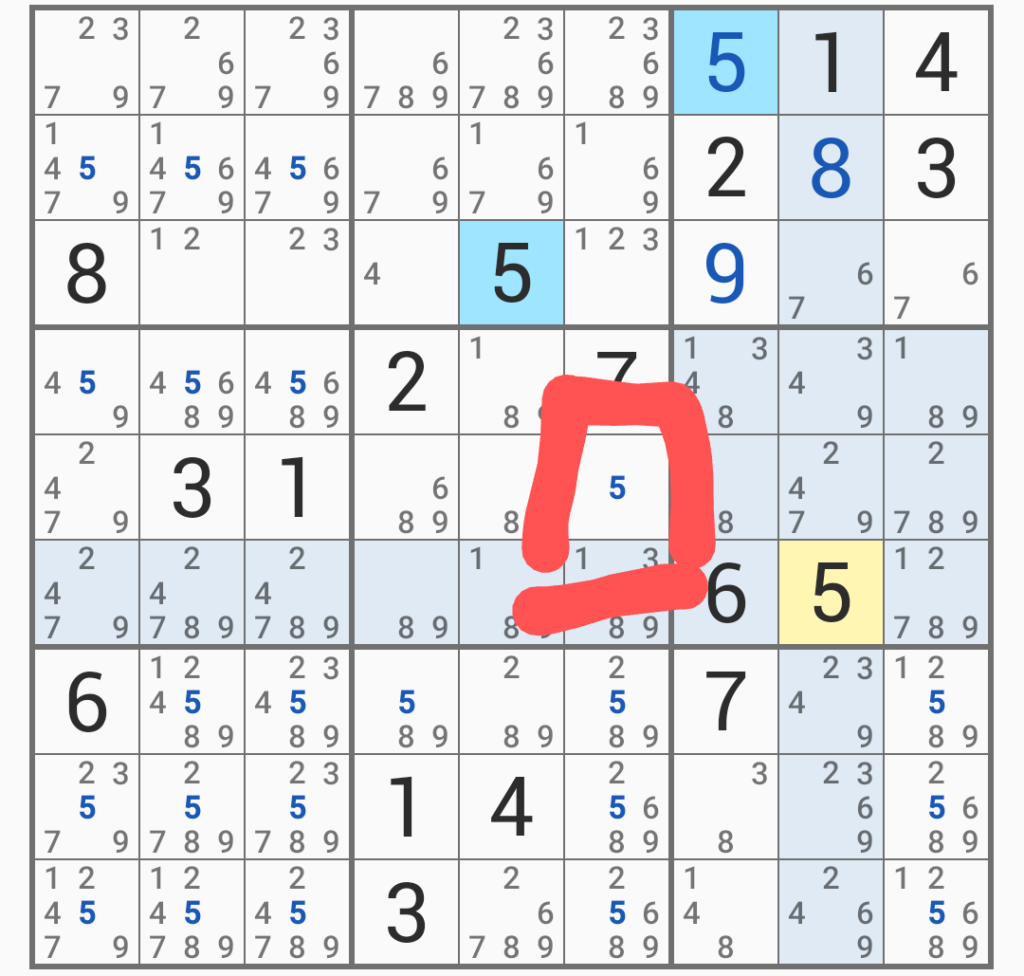
で、右側の方を「ここは5だ」と仮に確定する。「仮」なので、確定はせず、メモ機能で書くのみ。ただし、他の候補数を全て削除する(これが大事!)
ただし、同じマスには他の候補の数が「4、6、8、9」と4つもあったので、それをごっそり減らせたのが大きい。で、ここを「5」とした場合、盤面にどういう変化が出るのかを見ていく。
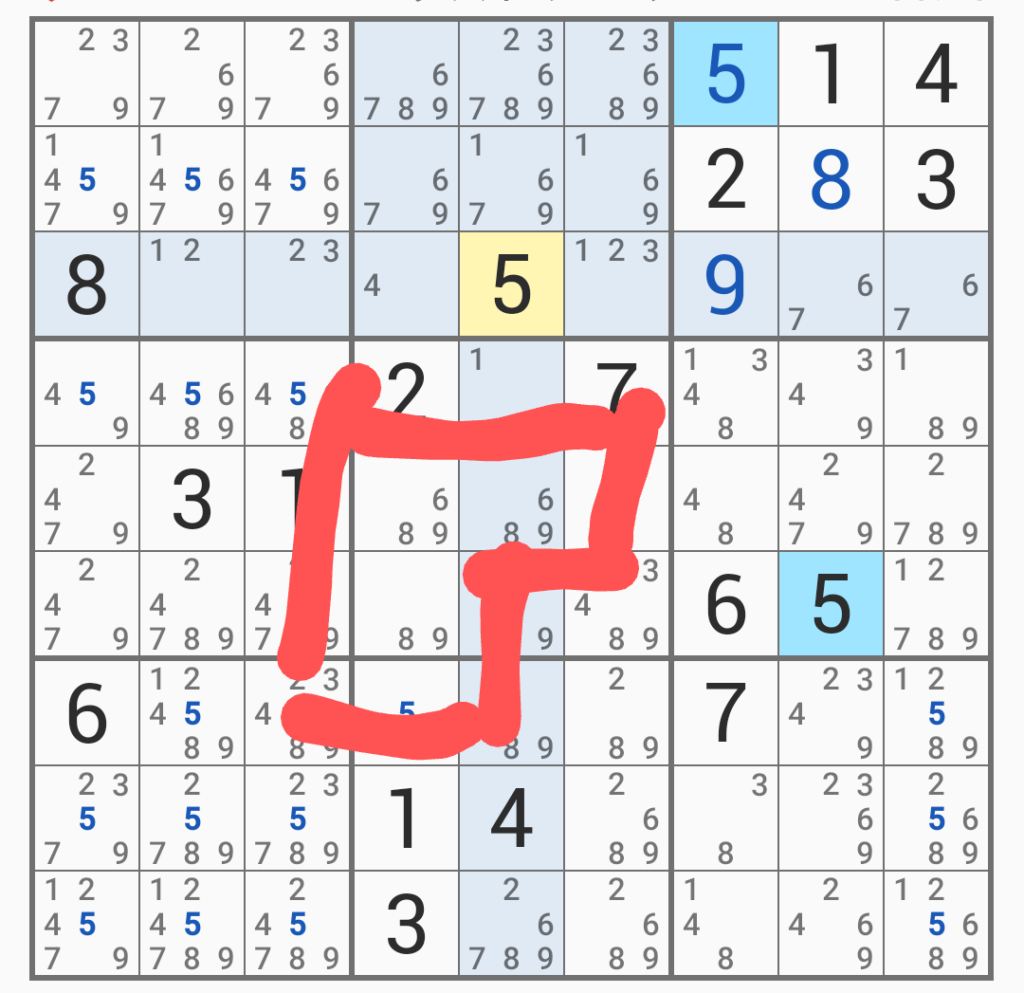
赤で囲ったところが、「6、8、9」「6、8、9」「8、9」となっているので、「6、8、9」の数字を占有できるため、同じ正方形内の「6、8、9」を除外する。
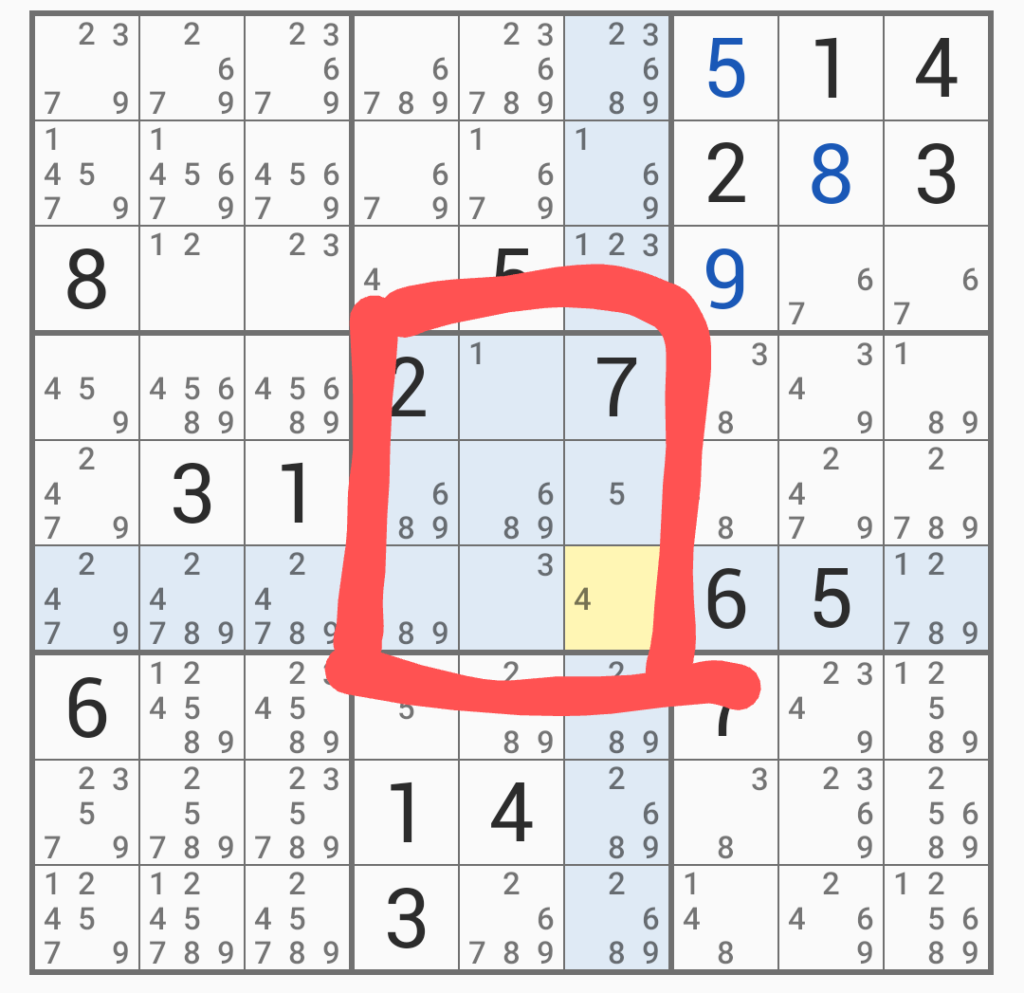
するとこうなって、単体の「3」「4」ができる。一歩前進である(仮だが)。この単体の数字を用いて、他のところにある数字を消して整理していく。
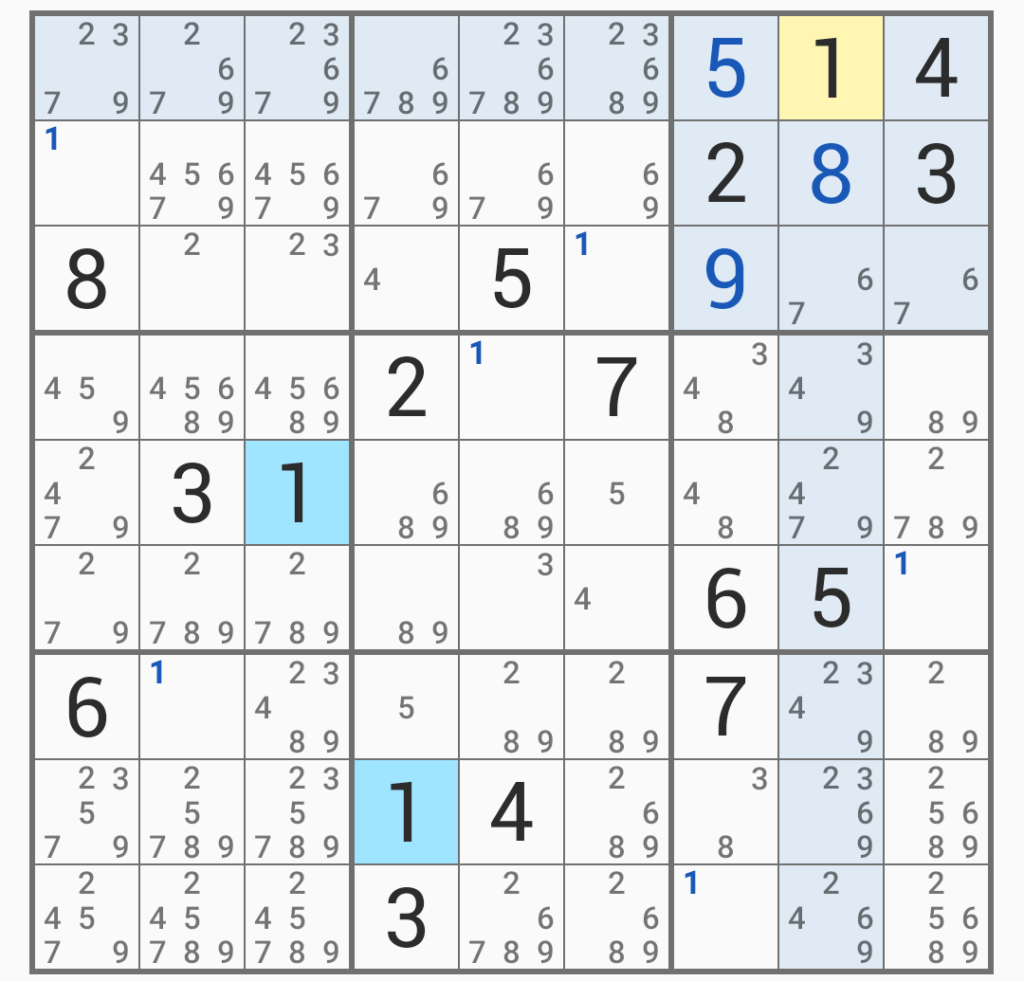
最初に「1」の位置が全て定まった。今回の「エクストリーム」では、「ある数字に着目し、その数字の位置を先に固めてしまう」というやり方でやっているのだが、これは効率がよいと感じる。
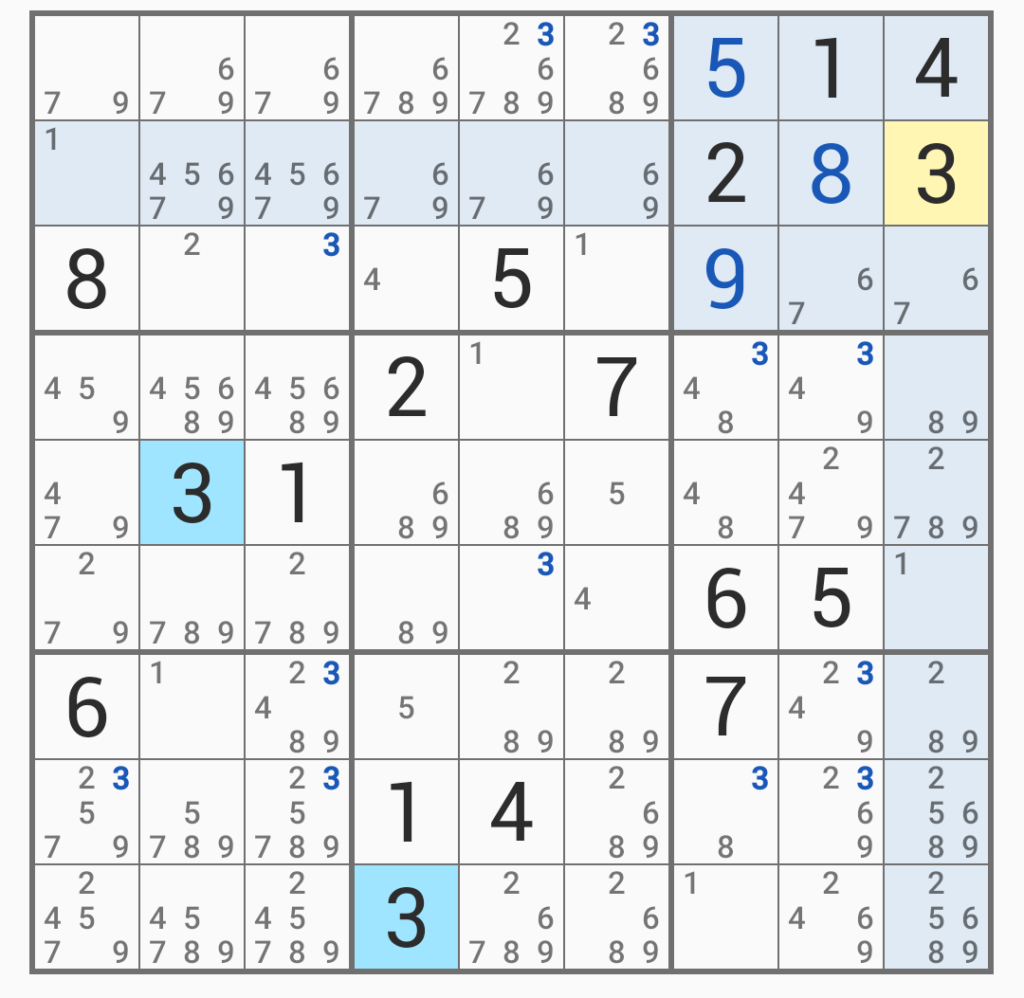
次に「3」がある程度定まったが、まだ仮確定できない部分もあるが、それはほうっておいて先に進む。
赤で囲ったところで「6、7、9」の占有がおきているため、同じ列、同じ正方形内で、重複する数字を消す。
するとこのように整理できるが、
ここで単体の「8」が出てきたので、これを使ってさらに整理すると、
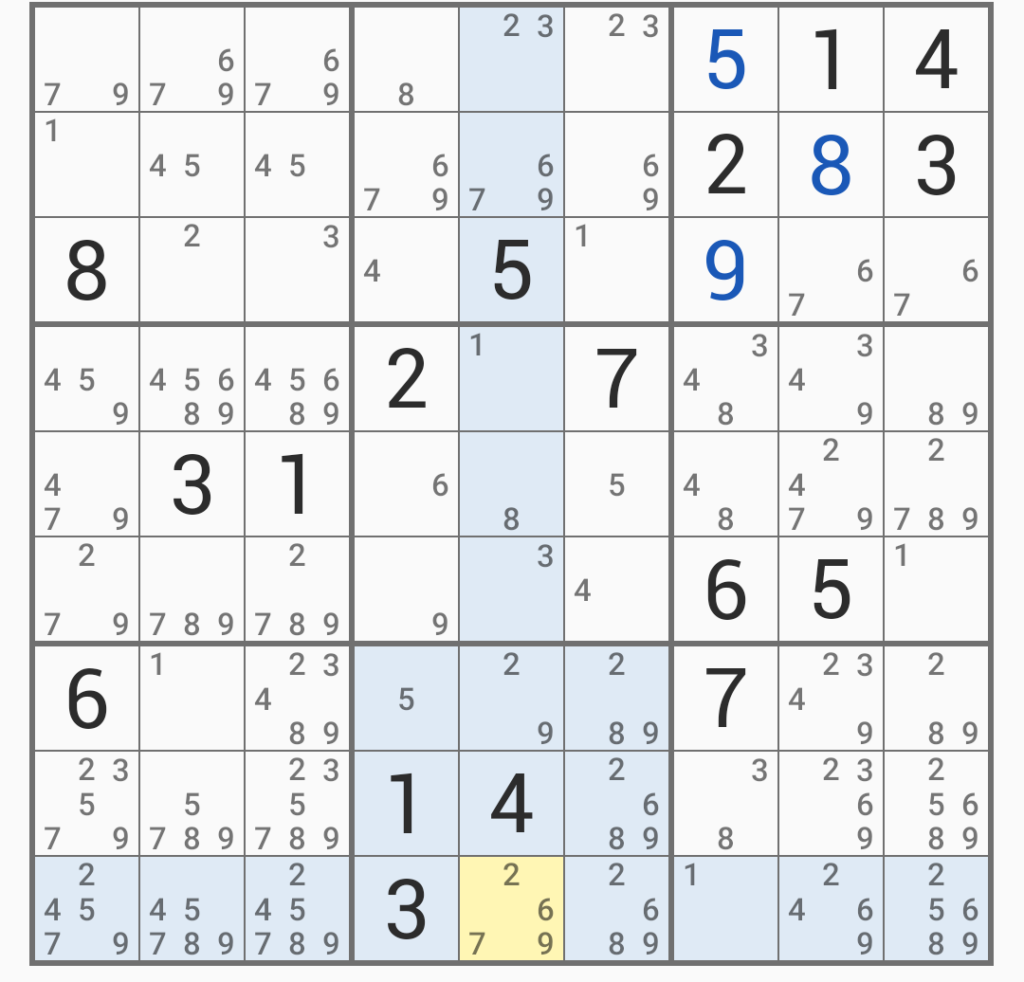
このようになる。
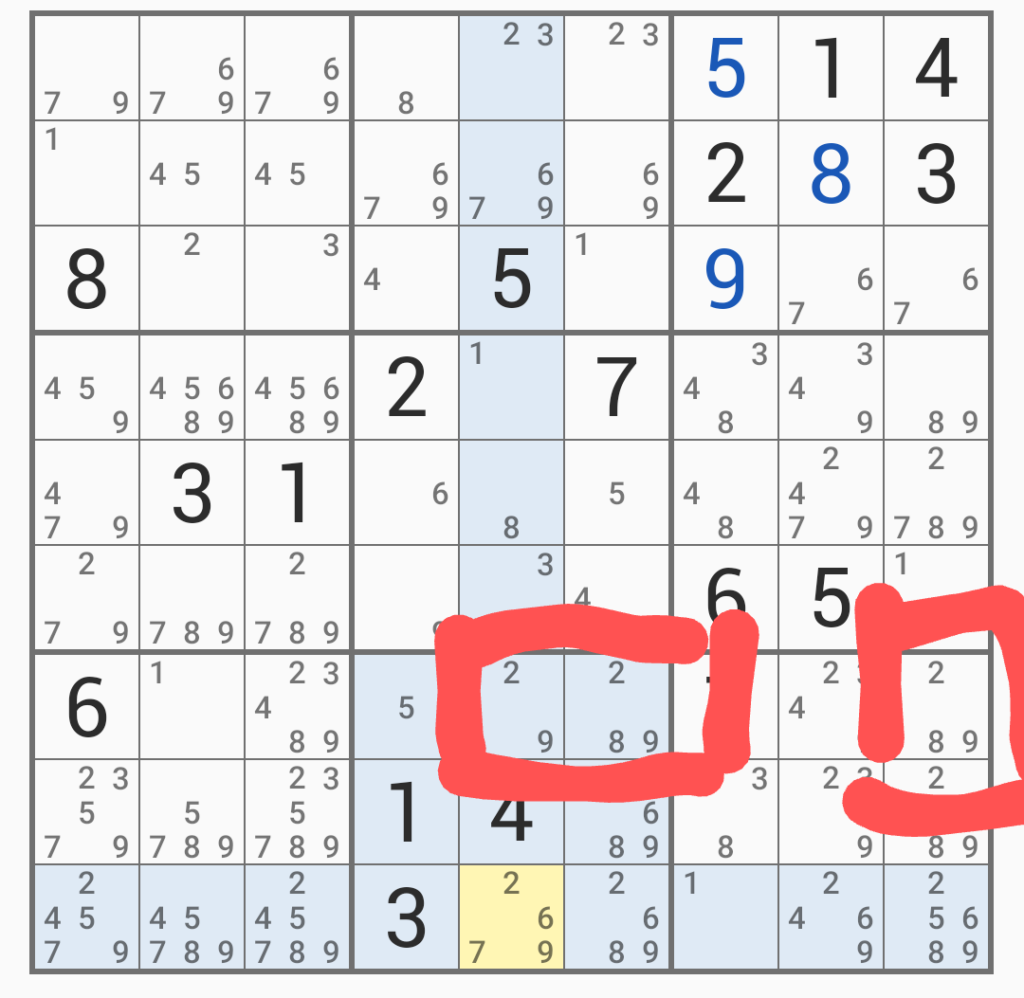
赤枠のところに着目すると、「2、9」「2、8、9」「2、8、9」で「2、8、9」の占有が起きているから、ここも同じ列の重複を消すことができる(正方形をまたがっているため、正方形内の数字は消せない)。
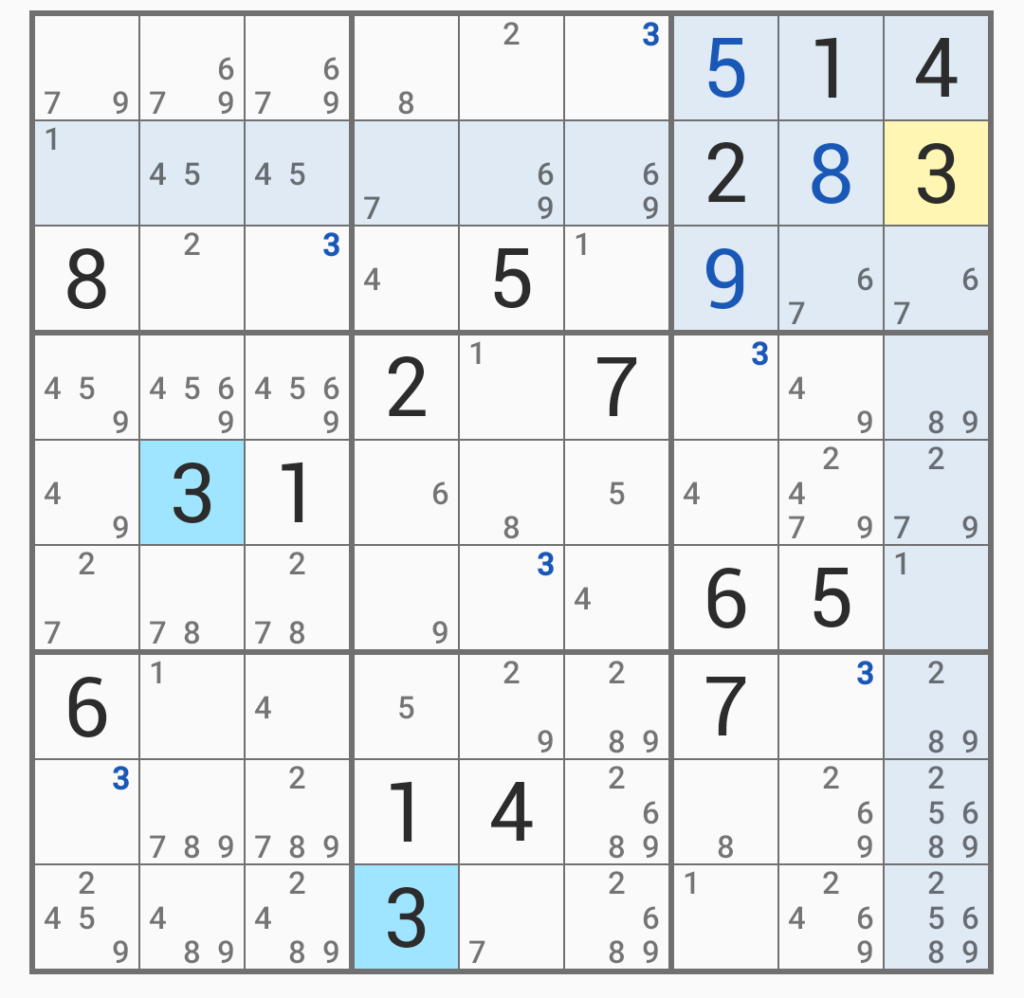
ここまでやって、さらに整理してようやく「3」の位置が全て定まった。
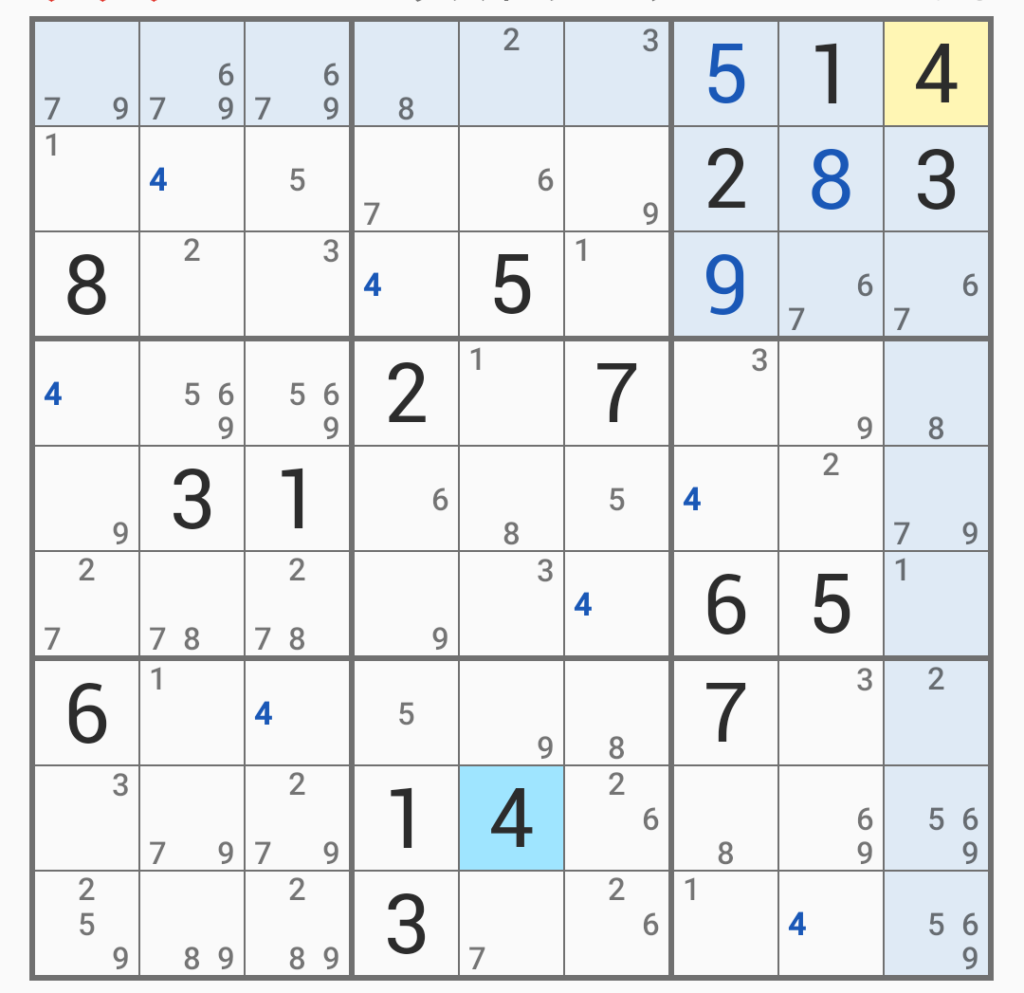
さらに整理していくと、次は「4」の位置が定まった。まだ矛盾は生じていない。
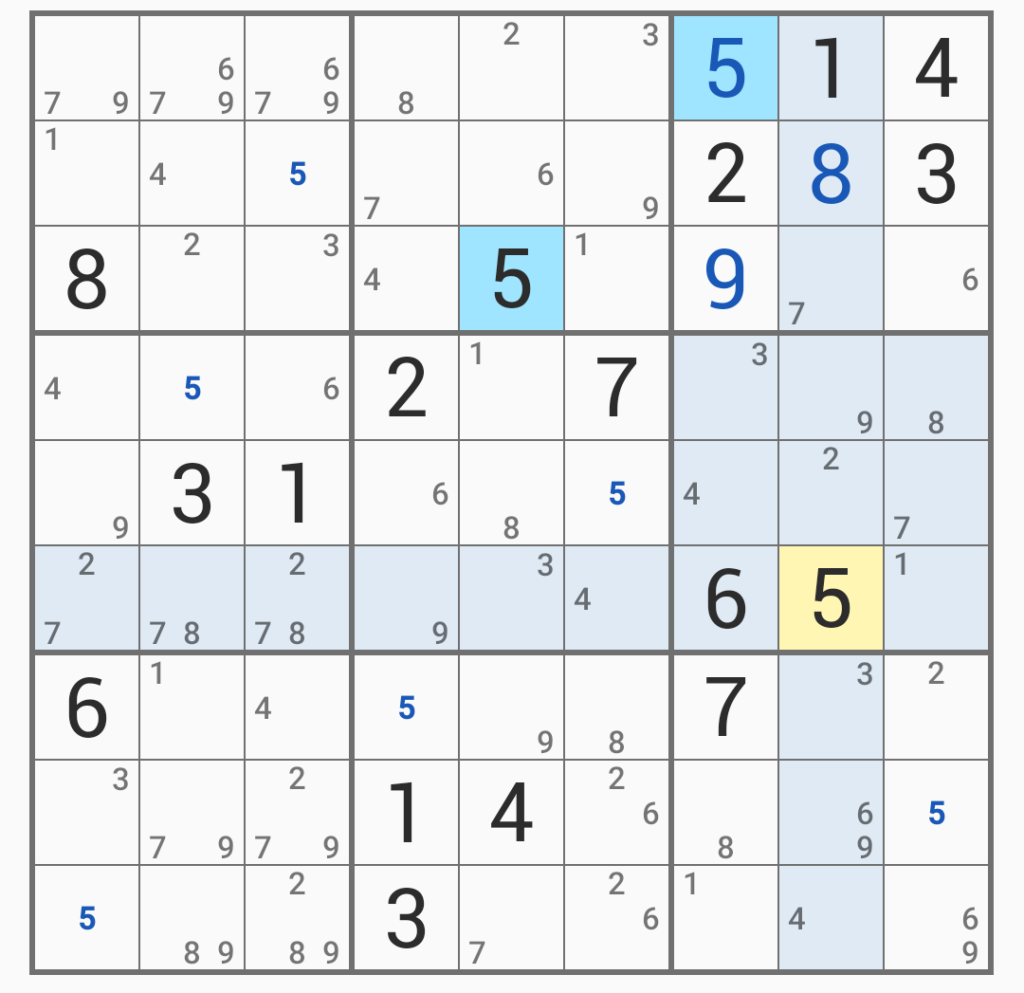
「5」が定まった。
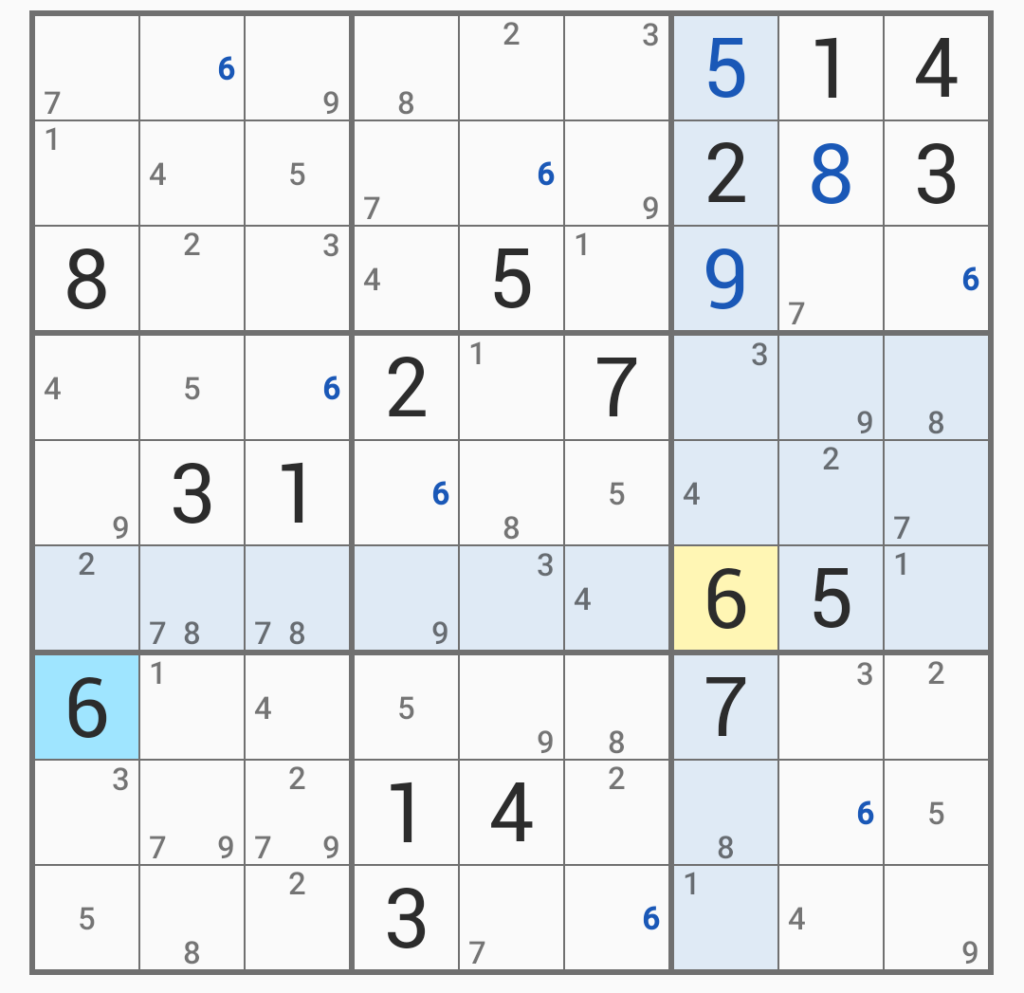
「6」が定まった。あと残るは「2」「7」「9」あたりの絡まりで、このへんが解ければいいのだが。
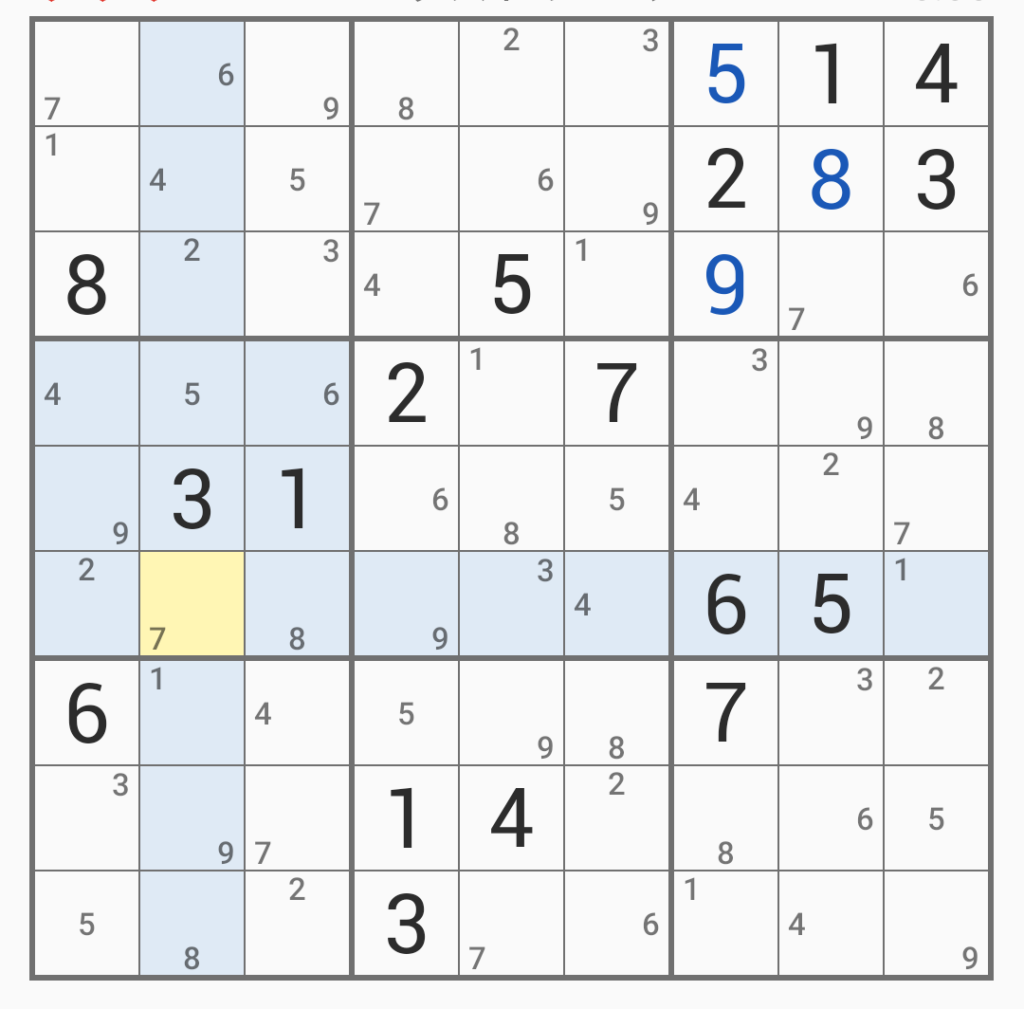
ようやく全てのマスが埋まった。
これを検証する。要は縦、横に重複する数字がないかを見ればよい。ないことを確認して確定する。
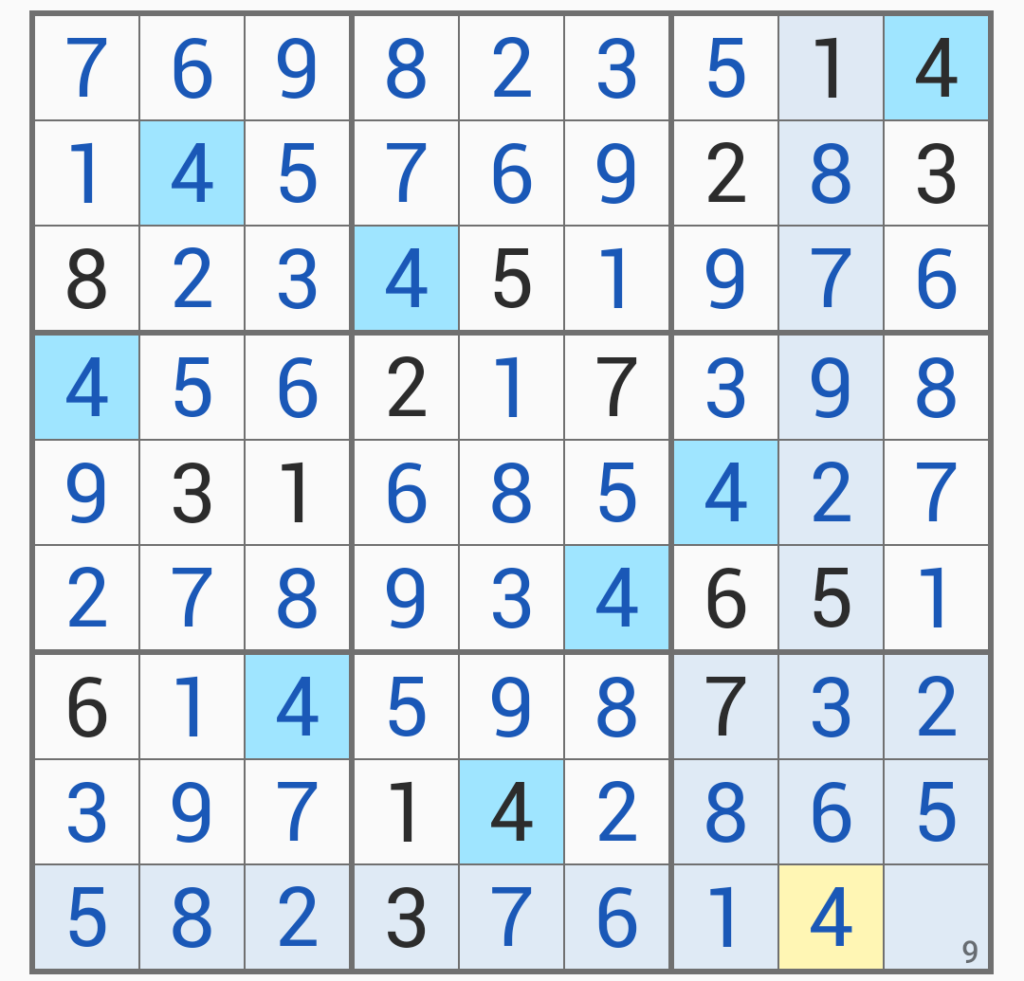
これで最後までいった。
今回は「仮定法で仮定した数字が結果的にあっていた例」である。
いくら複雑そうに見えても、細かい問題の積み重ねに落とし込んでしまえば、時間はかかるにしても解ける。
ということで、最近はまたエクストリームを一日1~2題解く日々である。


コメント