今回は
グダグダな状況から背理法を使って解けるか
という実験をしてみる。
先日は「背理法は終盤に使うとよい。できるだけ候補を絞ってからのほうがよい」
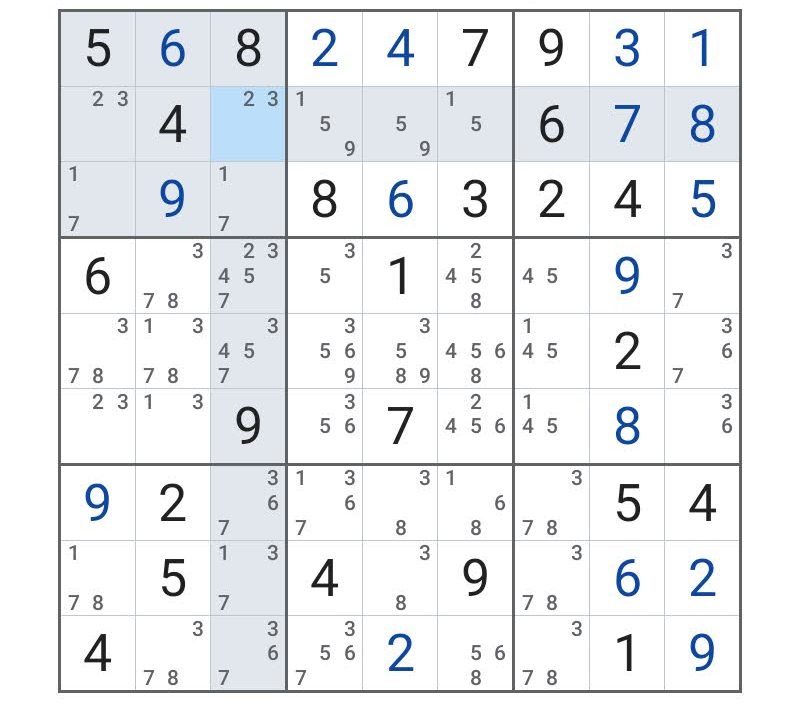
と書いたものの、この画面はこの時点で詰んでしまった。いろいろ未確定要素が多すぎる。
そこで、赤字の部分↓に注目してみる。
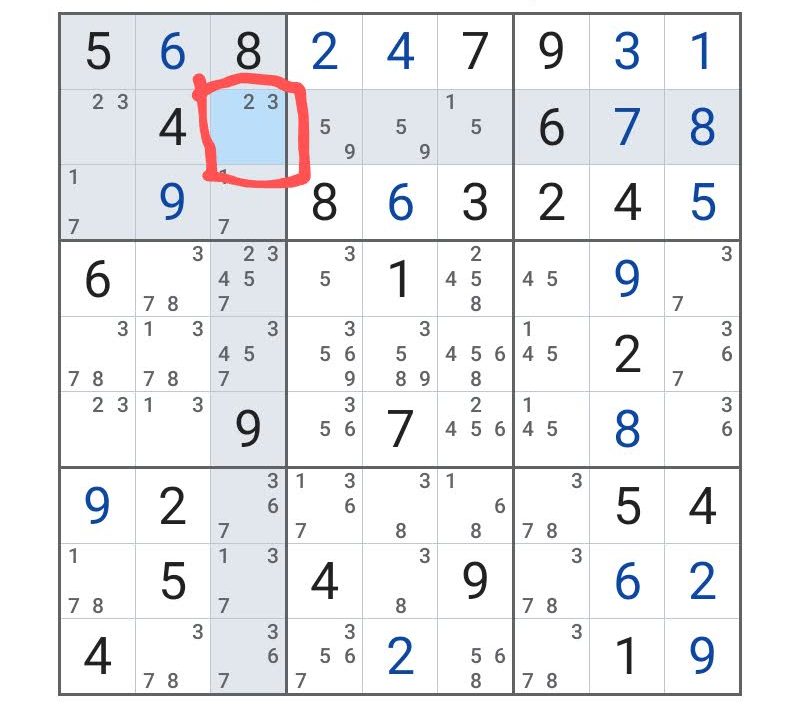
このマスは、ここだけ見れば「二択」なので、ここで「背理法」を使ってみる。
仮にこのマスを「3」だと仮定してしまう。そして、
確定しないマスはそのまま放っておいて、確定するところだけを埋めていくと、こうなった。
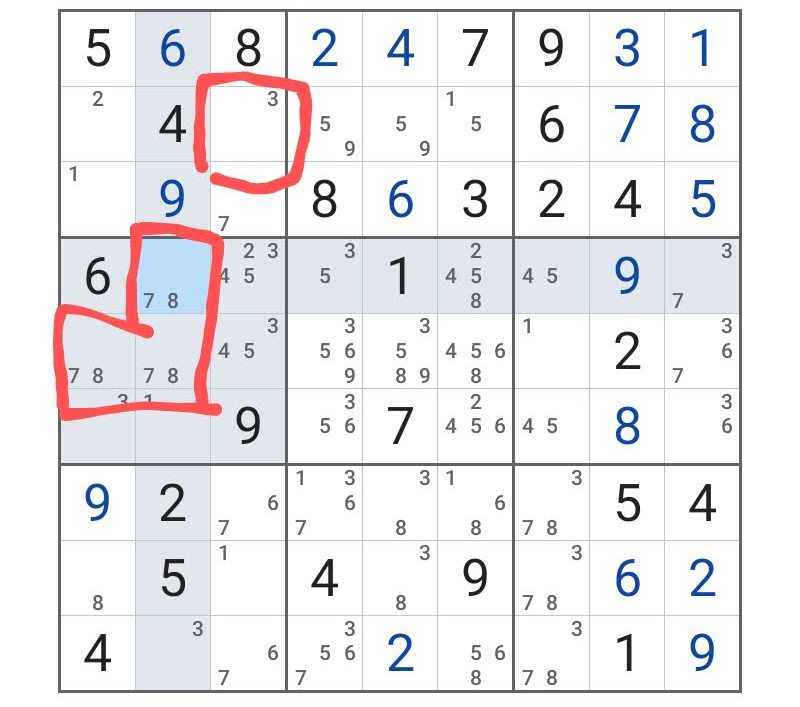
このとき、先ほどの赤で囲ったマスを「3」だとした場合、
この場合は逆時計回りに、左にいって、下にいって、右真ん中にいって・・・とやると、
「3」の左下に「7、8」のマスが3つできてしまう。
ということは、一つだけ、「空欄」のマスができてしまうことになって矛盾してしまう。
よって、先ほどのマスは
実は2だった。
ということが確定する。
メモを「元に戻す」機能を使って元に戻して、先ほどのマスが再び「2、3」になってから、ここを「2」で確定する。
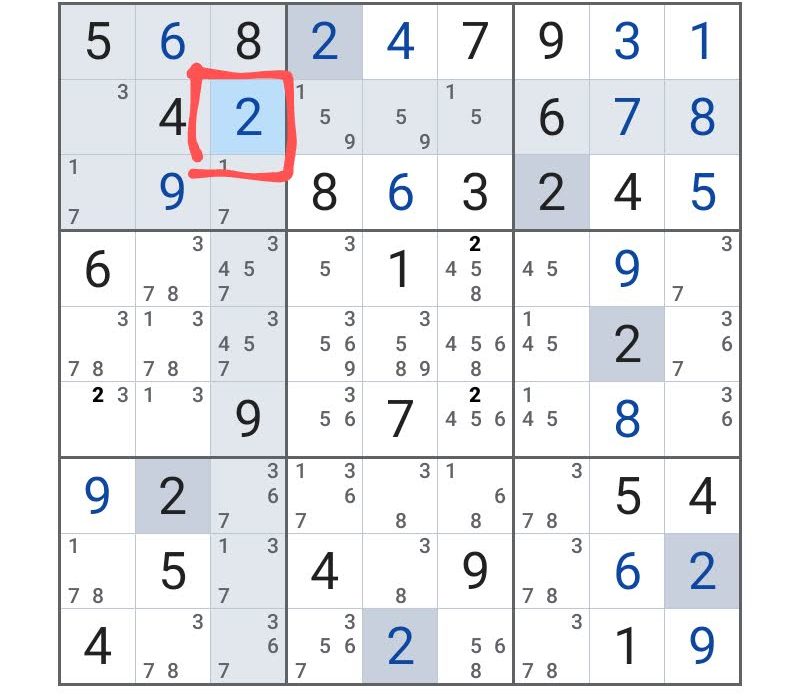
この状況から他に確定できる数字を埋めていくと、
「詰まり」はここだけであったらしく、最後まで行ってしまう。
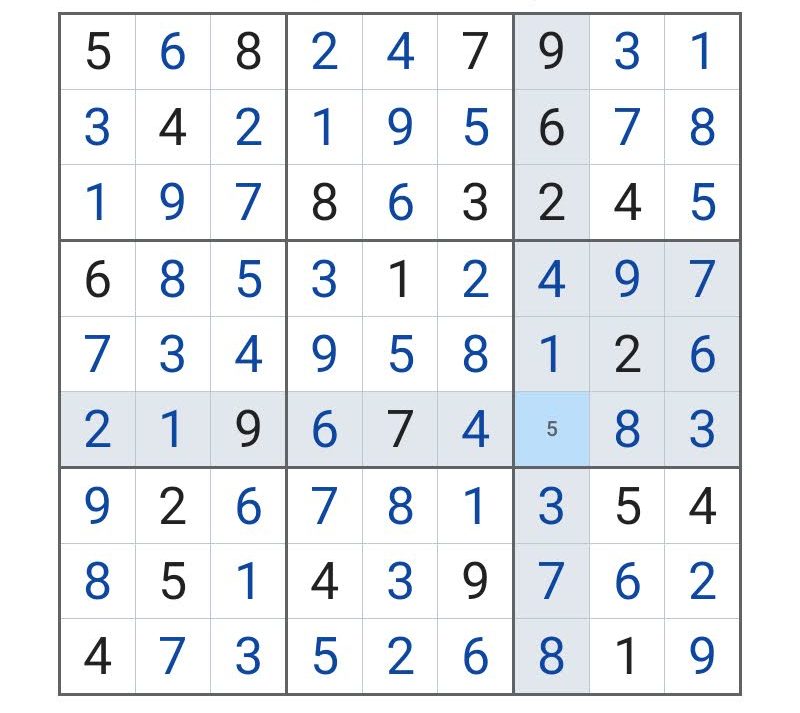
これで完成。
どうやら「背理法」は、「中盤でも使えることがある」ようだ。
もっとも、ここが確定したら後は芋づる式に解けたので、ここが実は「終盤」であった、ということなのかもしれないが、
とりあえず、
グダグダな状況からでもなんとかなる。
という例である。


コメント