「ナンプレ」(”Number Place”の略)というパズルゲームがある。
以前からやってみたかったのだが、やり方がわからず、せっかくアプリもたくさん出ているのにやり方の説明がなく・・ということでやれなかったのだが、先日、初心者向けの解説サイトをみつけた。
↑これは「数独」(「ナンプレ」の日本での登録商標)を開発した「ニコリ」のサイトである。ごく初歩的な解法だが、これでも何もないよりはマシである。
簡単に言えば、「9*9マス=81マスの縦・横に重複せずに1~9の数字を入れていき」、さらに「81マスの中にできる9つの正方形の中でも1~9までの数字を重複せずに入れる」、というパズルであり、「この法則性を満たした解を見つけよ」、という数学なのだ。
「上級編 解説サイト」も見たが、よくわからなかった。いや、意味はわかるのだが頭に入ってこないのである。
よく考えたら、将棋やオセロのアプリがあったからといって、いちいちコマの動かし方などが説明されているアプリがないのと同じことなのだろう。
そこで、とりあえず「場数」をこなしていくことにした。
そこでいくつかの法則性を発見したので、それをシェアしつつ、備忘録的に「ナンプレライブ」をやってみたら面白い(かつ自分のノート代わりになる?)のではないか、と考えた。
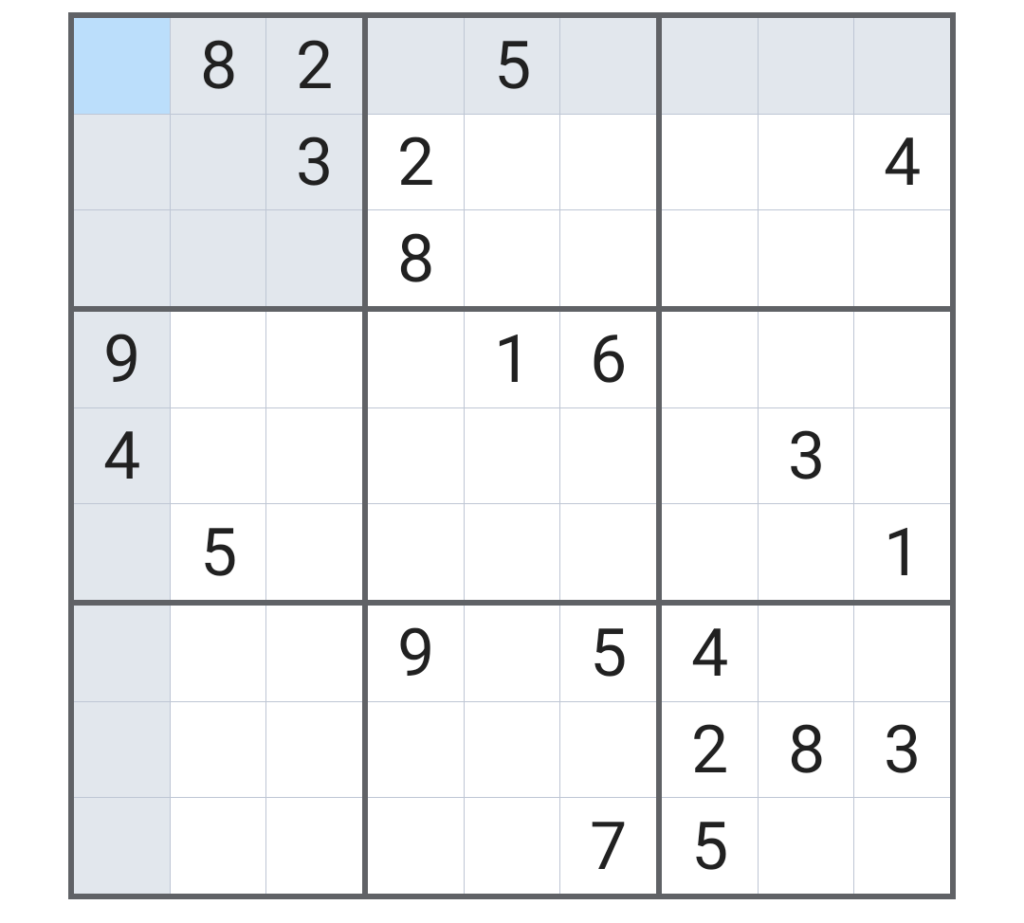
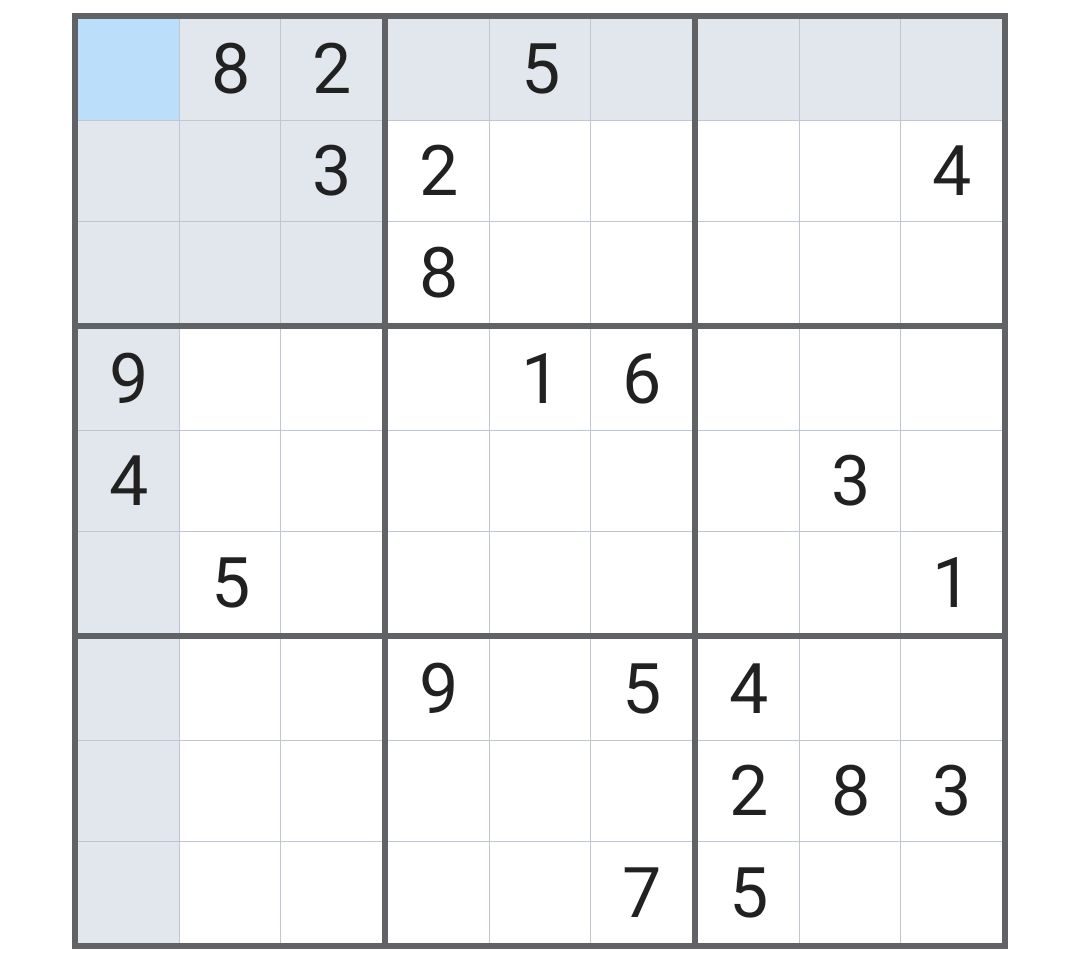
まず冒頭の画面が初期画面である。右端の「1」に注目して、「1」が入るマス(の候補)に「1」を埋めていく(なお、中級レベルくらいまでは「メモ機能」を使わずとも解けるが、上級以上は「メモ機能」なしでは解けないことがわかってきた)。
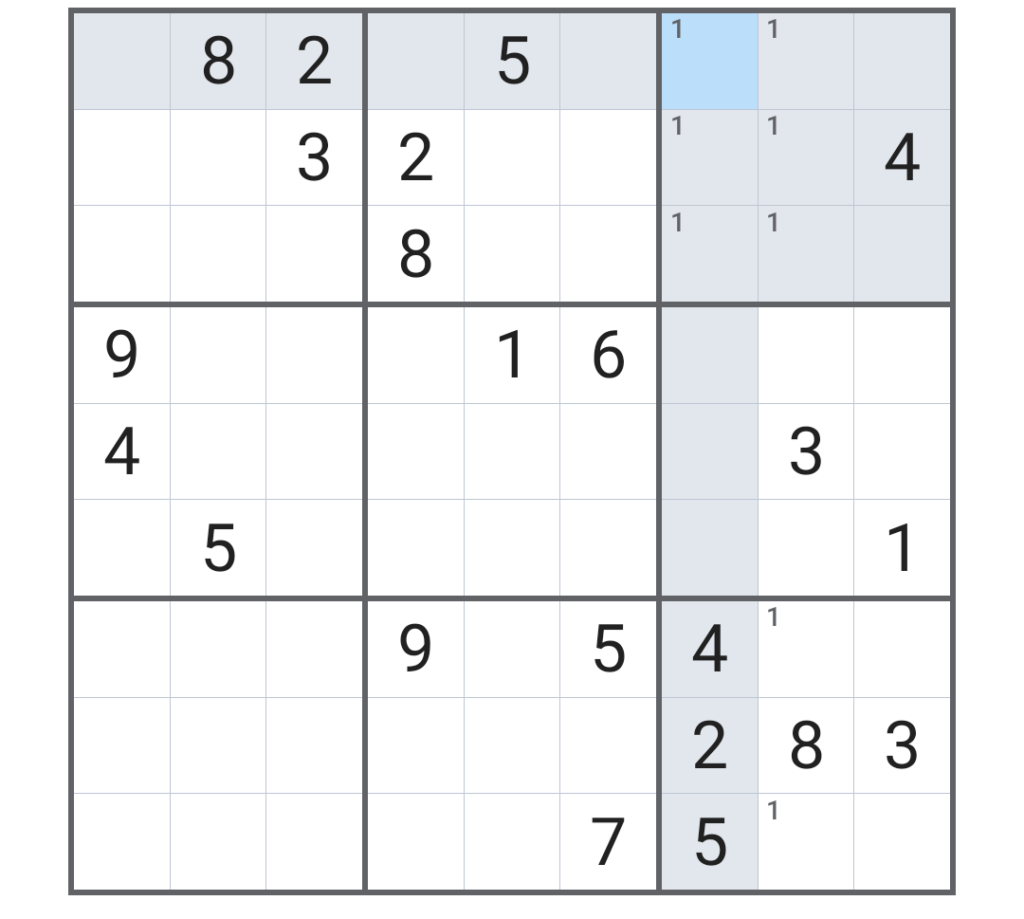
仮に横の列名を1~9で数えると、7~9列目に注目して、9列目にはすでに「1」があるため、「1」が入るのは7列目と8列目になる。
ところが、よく見ると8列目7~9行目は「1」が「ここにしか入らない」ため、自動的に「8列目の1」の位置がある程度決まってしまうのだ。そこでそれを踏まえて「8列目が埋まった」という前提で一番上の正方形のマスのメモを修正すると次のようになる。
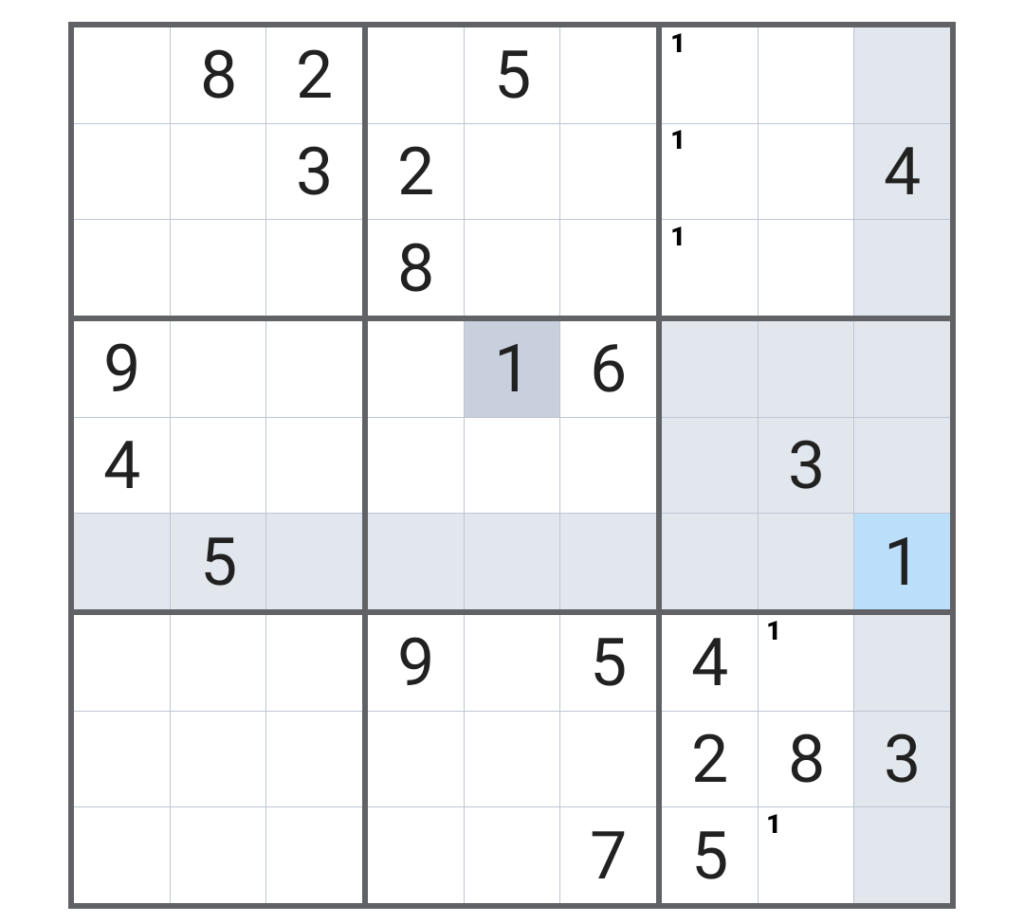
同様にして、「1」が入る候補のマスに全て「1」を埋めると、こうなる。
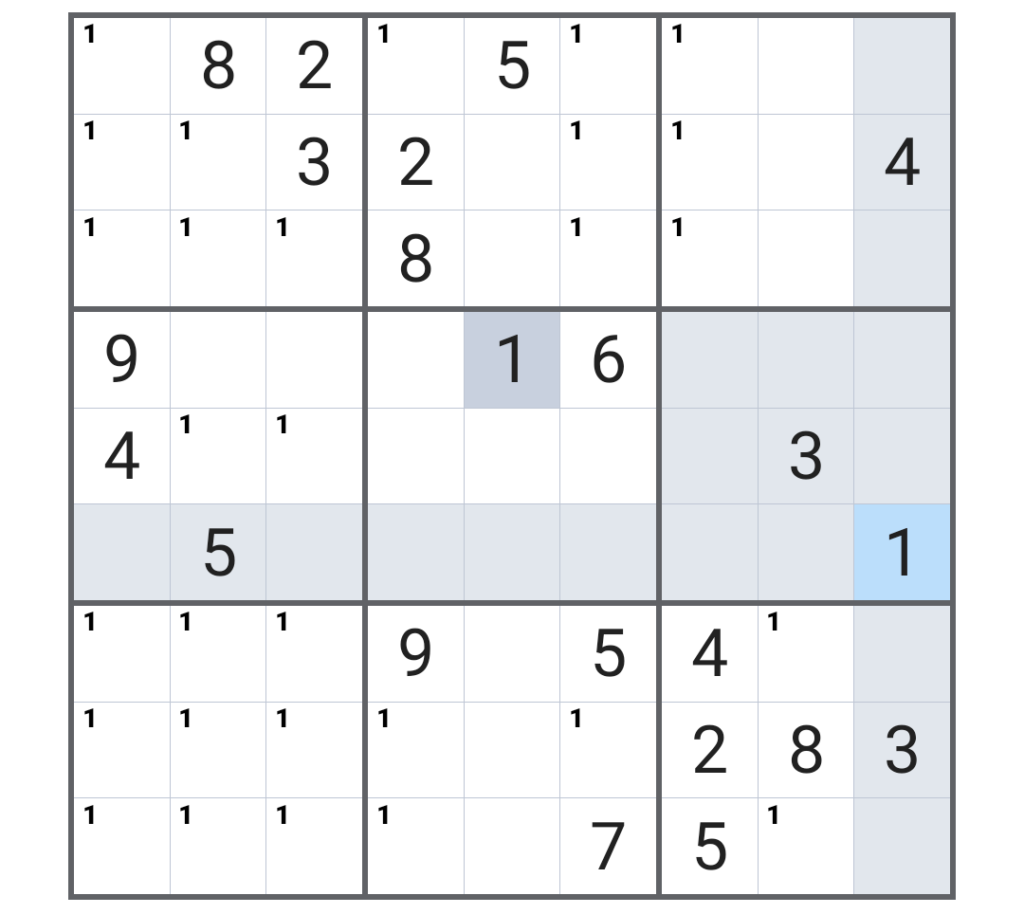
ようやく「1」の候補が全て埋まったので、この調子で「2~9」まで同様に埋めてみると、こうなる。
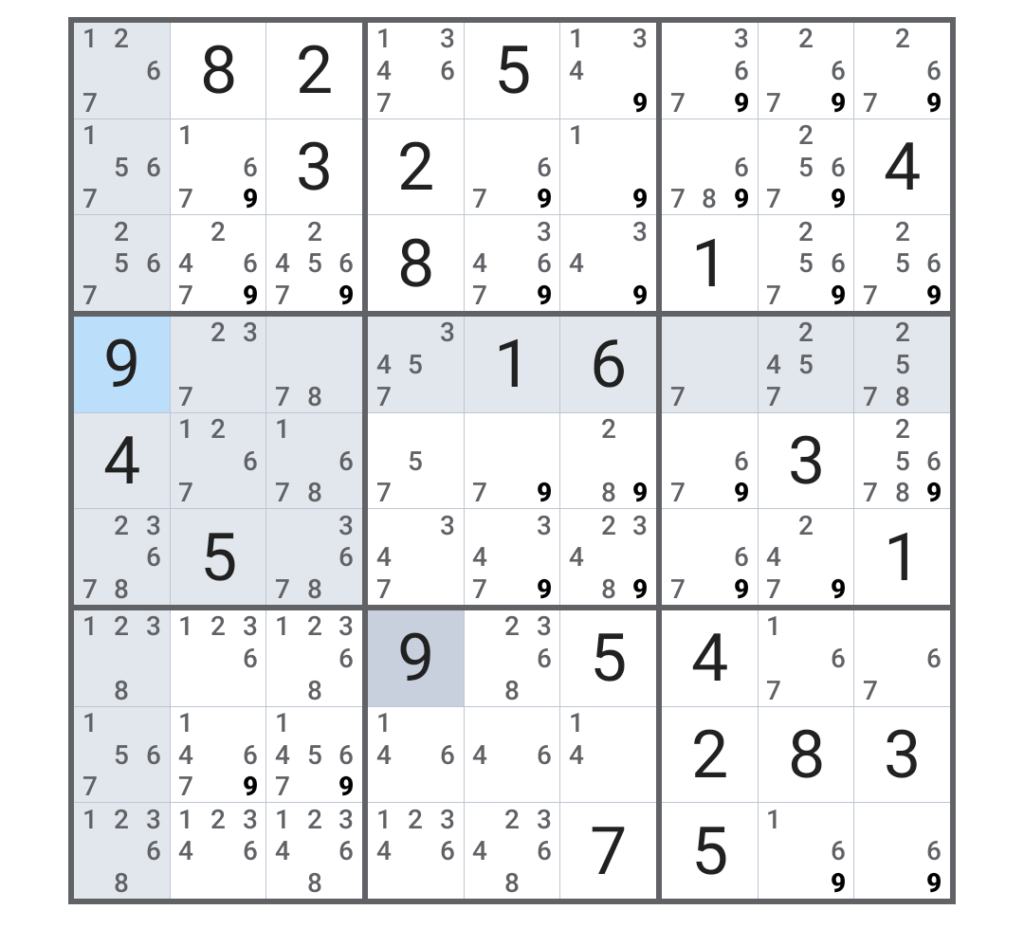
(個人的には、この図は「曼荼羅」とか「耳なし芳一」だな、とか思ってしまう・・・)
なお、横7列目縦3行目の「1」は、うっかり手が間違えて「1」をタップしてしまい、なお正解だったため、そこに残ってしまった・・。正解のマスは消せないのである。
さて、ここからでもぱっとわかることがある。
横7列目縦4行目のところに、ぽつんと「7」がある。ここは「7」で確定なのである。
ということで「7」をタップする。
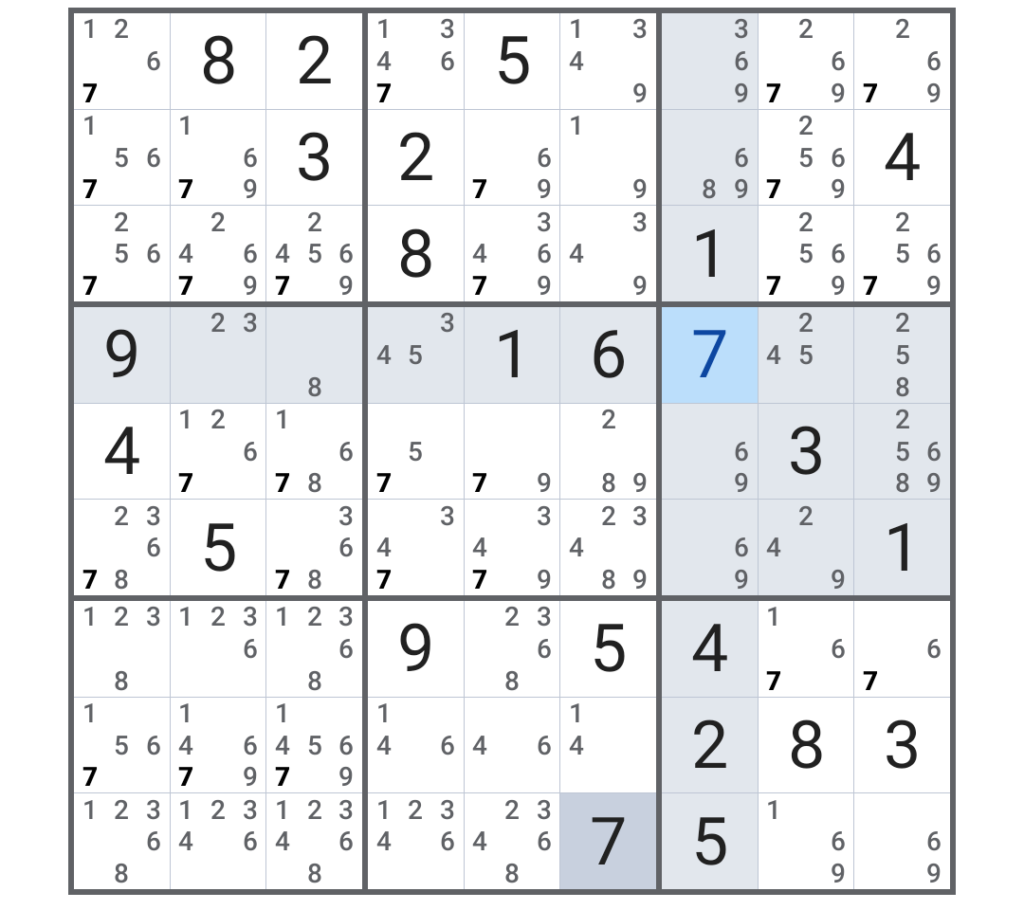
そうすると、好都合なことに、題材としてふさわしい数ができる。つまり、今の「7」の下に、
「6、9」というマスが2つできる。
ここで私の見つけた法則その1
数字「a、b」の候補が2つあれば、その2マスには「a、b」しか入らない
これは当たり前の話だが、片方を「a」とすればもう片方が「b」になるからである。それで何がわかるかといえば、
縦、あるいは横、あるいは所属している正方形のマスから「a、b」の候補を全て除外できる
ということだ。ここでは「6、9」なので、早速除外してみる。
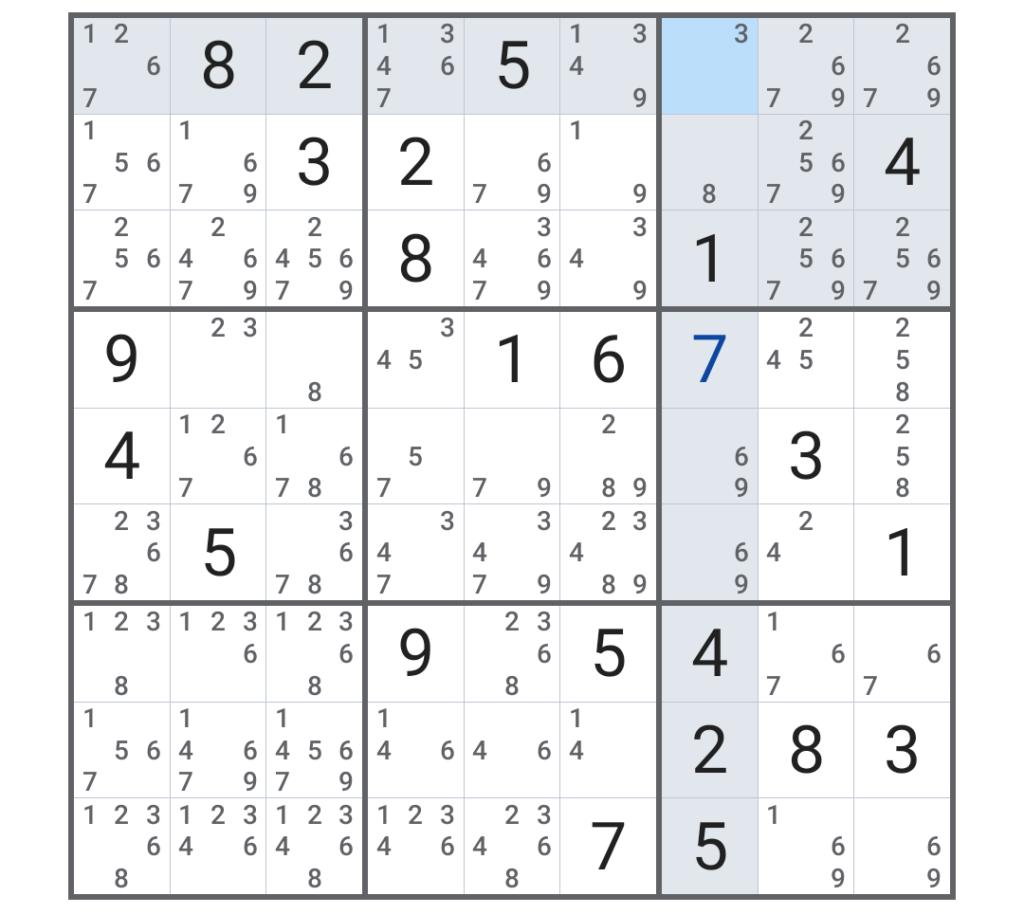
そうすると、幸い(?)この「6、9」という数字は縦列と正方形両方に所属しているので、そこから「6、9」の候補を除外すると、早速7列目の1行目=「3」、2行目=「8」がわかった。
なお、先程の「6、9」はそのままにしていいのか、といえば、とりあえずそのままにしておく。このようなものは次第にマスの数が減っていくとわかるようになっている。
また、横4~6列目、縦8行目の3つの数字に注目してみると、
「1、4、6」「4、6」「1、4」になる。
ここでまた私の見つけた法則その2
3マスにまたがって数字a、b、cが2つ以上候補になるときは、その3マスに入る数字はa、b、cになる
である。場合分けをして考えてみる。
- 「a、b」「b、c」「a、c」が候補のとき(候補が2、2、2のとき)
1つ数字を決めれば他が全部決まる。 - 「a、b」「a、c」「a、b、c」(候補が2、2、3のときその1)
- 「a、b」「b、c」「a、b、c」(候補が2、2、3のときその2)
- 「a、b」「a、b、c」「a、b、c」(候補が2、3、3のときその1)
- 「b、c」「a、b、c」「a、b、c」(候補が2、3、3のときその2)
- 「a、c」「a、b、c」「a、b、c」(候補が2、3、3のときその3)
- 「a、b、c」「a、b、c」「a、b、c」(候補が3、3、3のとき)
・・と、このような場合があるが、全てにおいて数字が一意的に定まる。最後は一意的には定まらないが、3マスに3つの数字しか入らないわけだから、これ以外の数字ははまらない。
また、「a、b」「a、c」「a、b、c」(候補が2、2、3のときその1)は、1番目が「b」だとした場合、2~3番目は「a、c」「a、c」になるが、その場合先程の「2マスのケース」に還元される(ただし一意的には定まらない)。それ以降も同様。
ということで、
再び、横4~6列目、縦8行目の「1、4、6」「4、6」「1、4」に注目すると、
「この3マスの中に、1、4、6ははまり、それ以外の横の列からは除外できる」となる。
ここまでを進めてみると、画面はこうなる。
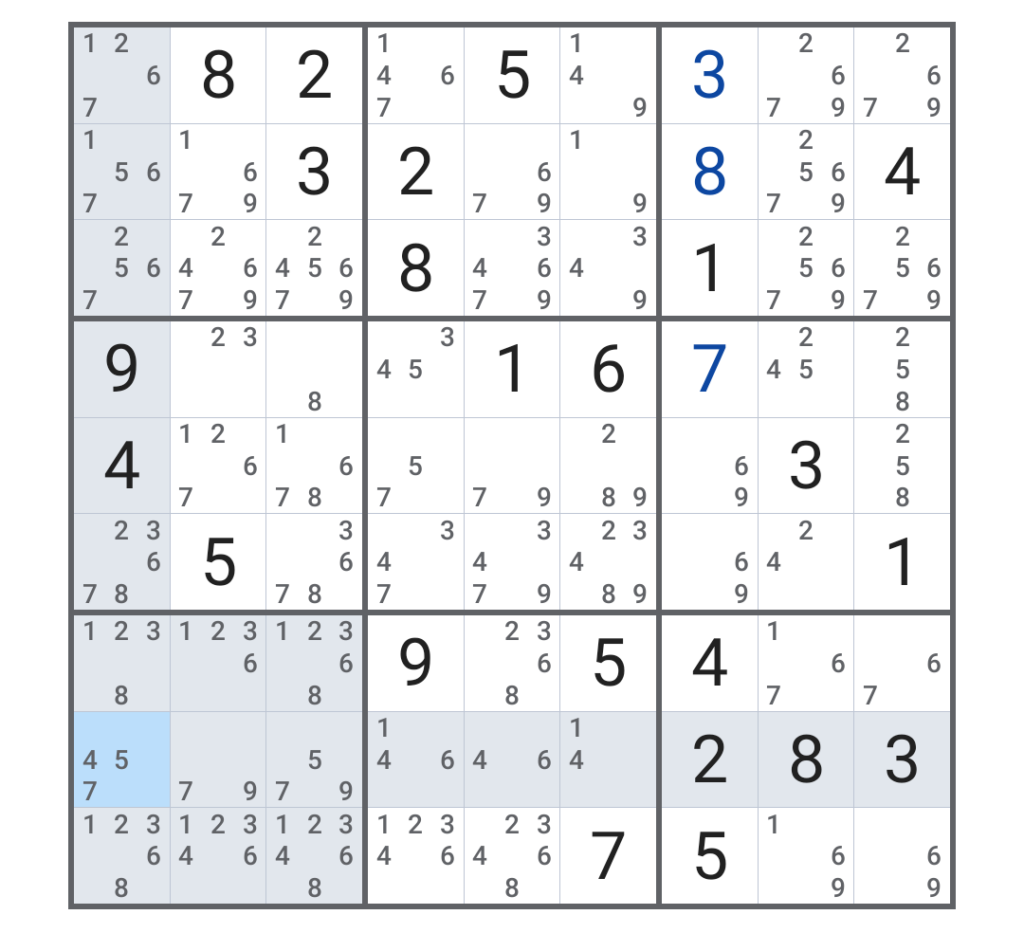
横3列目、縦4行目に「8」がポツンとあるので、そこを確定してみる。すると、画面に変化が現れるのだ!
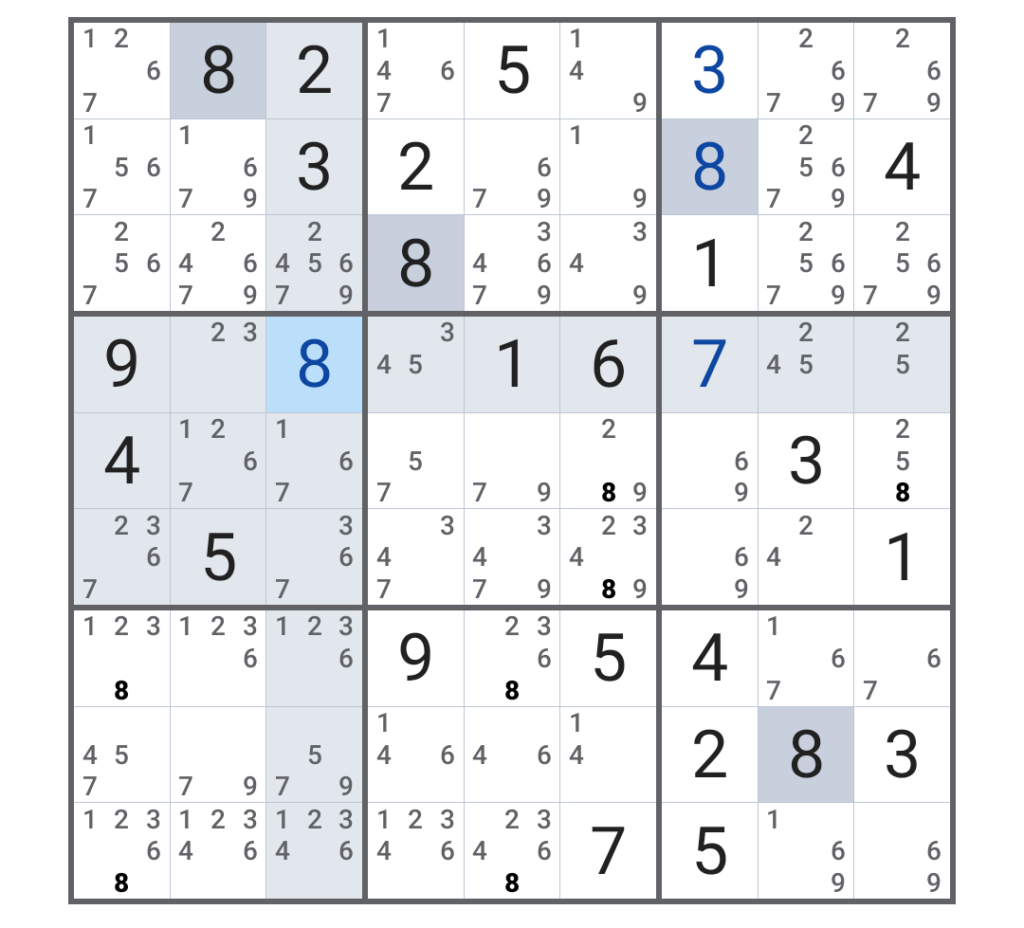
今、「8」の数字を太字表示にしているのだが、今埋めた正方形から右に視点をずらすと、右端の「8」が1つ浮いているではないか!
これは先程の画面では真上にも「8」があって確定していなかったものなのだが、それが別のマスが埋まったことで状況が変わるのである。この辺りはまるで将棋のような感じだ。
当然その「8」をタップして戦局(?)を動かす。
自分の感覚が合っているのかどうかはわからないが、
- 2マスの同数(はまる2つの数)を見つけ出し、他のマスから除外
- 3マスの同数(はまる3つの数)を見つけ出し、他のマスから除外
- 数字が一つ埋まったらまた盤面を見渡す(盤面の変化の再確認)
の繰り返しで解けるようである。
とりあえず行けるところまで進めてみよう。
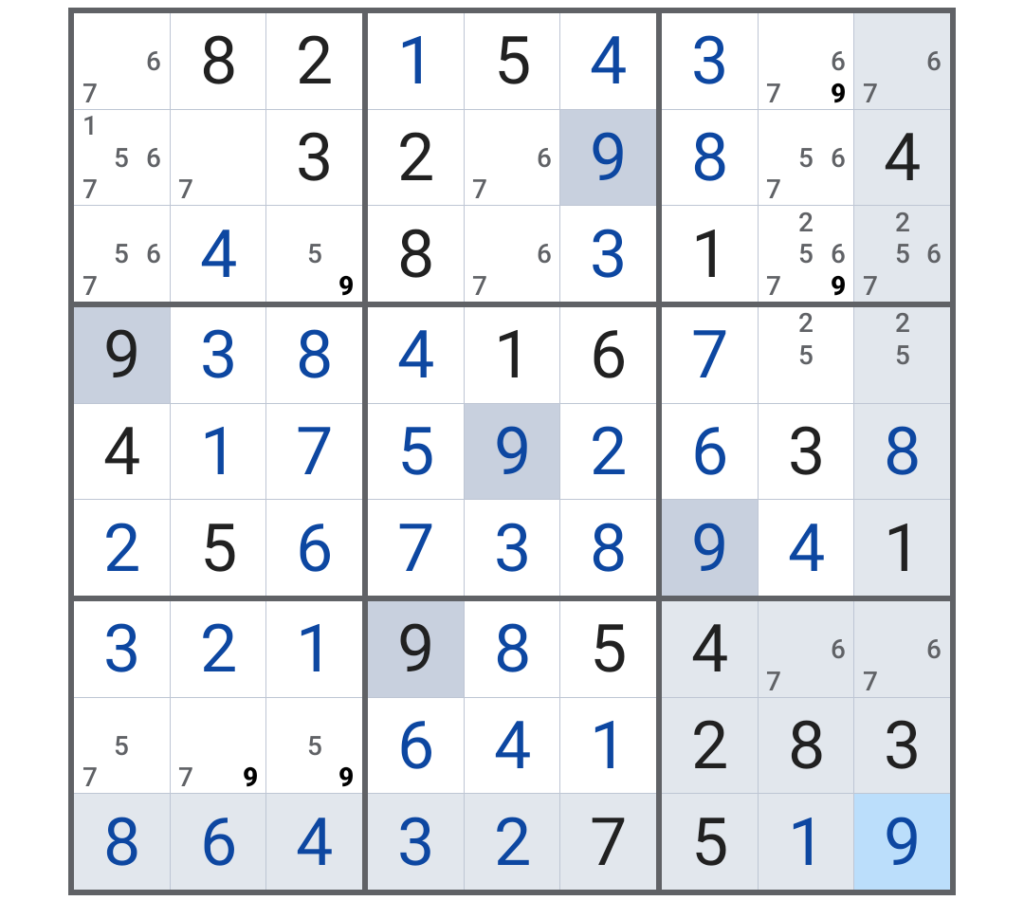
かなり埋まった段階。後半戦である。
ぱっと見ただけでも、縦2行目、横2列目に「7」がポツンとある。そしてその右斜め下には「9」が! まだまだいける!
対照的に、右端のほうを見ると「2、5」「6、7」がそれぞれ2マスずつあるが、これは進むと解決するはず。
ほぼ最終段階。左のほうは全て埋まって、残りは右端のみ。
あとは機械的に埋める作業。
これでラスト!
お疲れ様でしたm(_ _)m
※なお、最初のメモ書きには結構ミスがあるものである。あまり気にしてはいけない!
補足:上記の難易度は「上級」より上の「エキスパート」である。この上に「ジャイアント」という難易度がある。今は「エキスパート」で修行中(なんの?)。
コメント